-
Треугольник ABC задан координатами своих вершин. Высота AD и медиана AE пересекает сторону BC в точках D и E соответственно. Требуется
1. найти длину DE ;
2. составить уравнение прямой , проходящей через точку E параллельно AC;
3. найти внутренний угол B;
4. найти уравнение и длину биссектрисы AL;
5. составить систему линейных неравенств , определяющую внутреннюю область ABC.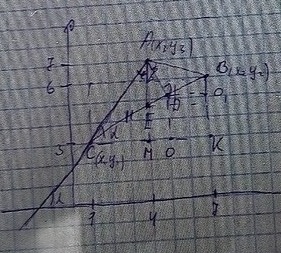
-
Предмет:
Математика -
Автор:
willowqdht - 6 лет назад
-
Ответы 1
-
1. найти длину DE.Находим координаты точки Е как середину стороны ВС:Е((7+1)/2=4; (6+3)/2=4,5).Координаты точки Д находим как точку пересечения прямой ВС и высоты АД. Уравнение
-3x+21 = -6y+363x-6y+15=0 сократим на 3 и получим уравнение общего вида:х-2у+5 = 0 или в виде уравнения с коэффициентом у = 0,5х + 2,5.Уравнение высоты АД:
.Подставим координаты точек:АД:
6x-24 = -3y+216x+3y-45 = 02x + y - 15 = 0 или y = -2x + 15.Решаем систему
Вычтем из первого уравнения второе -2,5х+12,5=0х = 12,5/2,5 = 5.у = -2*5 + 15 = -10 + 15 = 5.Отсюда находим длину отрезка ЕД:
≈ 1,118034.2. составить уравнение прямой , проходящей через точку E параллельно AC.Для этого надо составить уравнение прямой АС: АС : -4 Х + 3 У - 5 = 0 или, умножив на -1: АС: 4х - 3у + 5 = 0.Это же уравнение в виде уравнения с коэффициентом:у = (4/3)х + (5/3). Уравнение прямой , проходящей через точку E параллельно AC, имеет вид ах + в, где коэффициент а равен коэффициенту прямой АС.Подставим координаты точки Е:4,5 = (4/3)*4 + в.Отсюда находим значение в:в = 4,5 - (16/3) = -5/6.Получаем искомое уравнение у = (4/3)х - (5/6).3. найти внутренний угол B.Внутренние углы определяем по теореме косинусов. cos В= (АВ²+ВС²-АС²)/(2*АВ*ВС) = 0.70710. B = arc cos 0,70710 = 0.785398 радиан = 45 градусов.4. найти уравнение и длину биссектрисы AL.Уравнение биссектрисы имеет вид: АL: (((Ув-Уа)/АВ) +( (Ус-Уа)/АС )) * Х + ((( Ха-Хв)/АВ) + ((Ха-Хс)/АС)) * У + ((Хв*Уа - Ха*Ув)/АВ) + (Хс*Уа - Ха*Ус)/АС)) = 0.Подставив координаты точек, полчаем: -1,1162 Х + -0,34868 У + 6,90569 = 0 или, сократив на -1,1162: Х + 0,31238 У - 6,18664 = 0.Это же уравнение в виде уравнения с коэффициентом: у = -3.201265367 х + 19.80506.5. составить систему линейных неравенств , определяющую внутреннюю область ABC. x y т.С 1 3 АВ : -3.75 <0 т.А 4 7 ВС : 15 >0 т.В 7 6 АС : -15 <0
-
Автор:
carson544 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Привет, подскажите где можно начертить такой график можно
-
Предмет:
Математика -
Автор:
randall99 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Как переводится слово Japanese?
-
Предмет:
Английский язык -
Автор:
kayleyrcib - 6 лет назад
-
Ответов:
5 -
Смотреть
-
-
Задайте вопрос из школьного предмета
1-4 Математика 5+3 б
экскурсанты, указывая на скелет, спросили у сторожа музея:《сколько лет этому динозавру?》- 《Один миллион тридцать четыре года》. - 《Откуда Вы так точно
знаете его возраст?》 - 《Это просто!-ответил сторож. - Когда 34 года назад я пришёл сюда работать, мне сказали, что этому диназавру миллион лет》. Правильно ли рассуждал сторож?-
Предмет:
Математика -
Автор:
budda18 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Какую часть часа составляют 30 минут?15 минут?10 минут?6 минут Какую часть суток составляет 1 час?2 часа?2 1/2 часа?5 1/3 часа? Люди добрые! Помогите пожалуйста! ПОЖАЛУЙСТА!!!
-
Предмет:
Математика -
Автор:
bella53 - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
