-
Решить интеграл (Интегральное исчисление функции одной переменной)
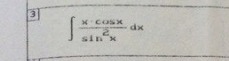
-
Предмет:
Математика -
Автор:
kaufman - 6 лет назад
-
Ответы 1
-
-
Автор:
blayne - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Исправьте речевые ошибки в предложениях.Назовите тип ошибок
1.Только что прошел сильный,проливной дождь
2.У матери отлегло сердце,когда она увидела Павла живым и невредимым
3.Небо затянуло сплошным серым облаком-
Предмет:
Русский язык -
Автор:
diegomzc9 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
сосуд имеет форму цилиндра высота которого равна h см а радиус r см где 25 < h < 26, 15 < r < 16 см. Зная что обьём цилиндра вычисляется по формуле [tex]V = \pi r^2h и 3.14\ \textless \ \pi \ \textless \ 3.15[/tex] , оцените вместимость сосуда
-
Предмет:
Алгебра -
Автор:
cindy lou who - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- 50 баллов!!!Вычислите массовую долю меди в его составе с кислородом , в которой медь проявляет степень окисления +1
-
30 БАЛЛОВ
Решить уравнение:
2sin^2x+3cosx=0
How much to ban the user?
1 hour
1 day
100 years
