Задать вопрос Регистрация
Помочь другим

  • Исследовать на сходимость несобственный интеграл, не вычисляя его.

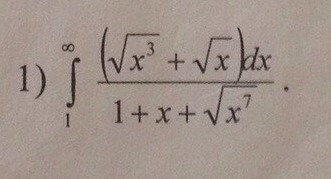
    question img

Ответы 1

  • \displaystyle \int\limits^\infty_1 {} \frac{ \sqrt{x^3}+ \sqrt{x} }{1+x+ \sqrt{x^7} } \, dx =\int\limits^\infty_1 {} \frac{\sqrt{x^3}}{1+x+\sqrt{x^7}}} \, dx +\int\limits^\infty_1 { \frac{ \sqrt{x} }{1+x+ \sqrt{x^7} } } \, dx \dfrac{\sqrt{x^3}}{1+x+\sqrt{x^7}}} \leq \dfrac{1}{x^2} Этот несобственный интеграл сходится по первому признаку сравнения\dfrac{\sqrt{x}}{1+x+\sqrt{x^7}}} \leq \dfrac{1}{x^3} сходится по первому признаку сравненияЗначит, данный несобственный интеграл сходится

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years