Задать вопрос Регистрация
Помочь другим

  • Помогите решить кто может. Для экзамена надо.
    Пользуясь формулой Ньютона-Лейбница, вычислить определенный интеграл.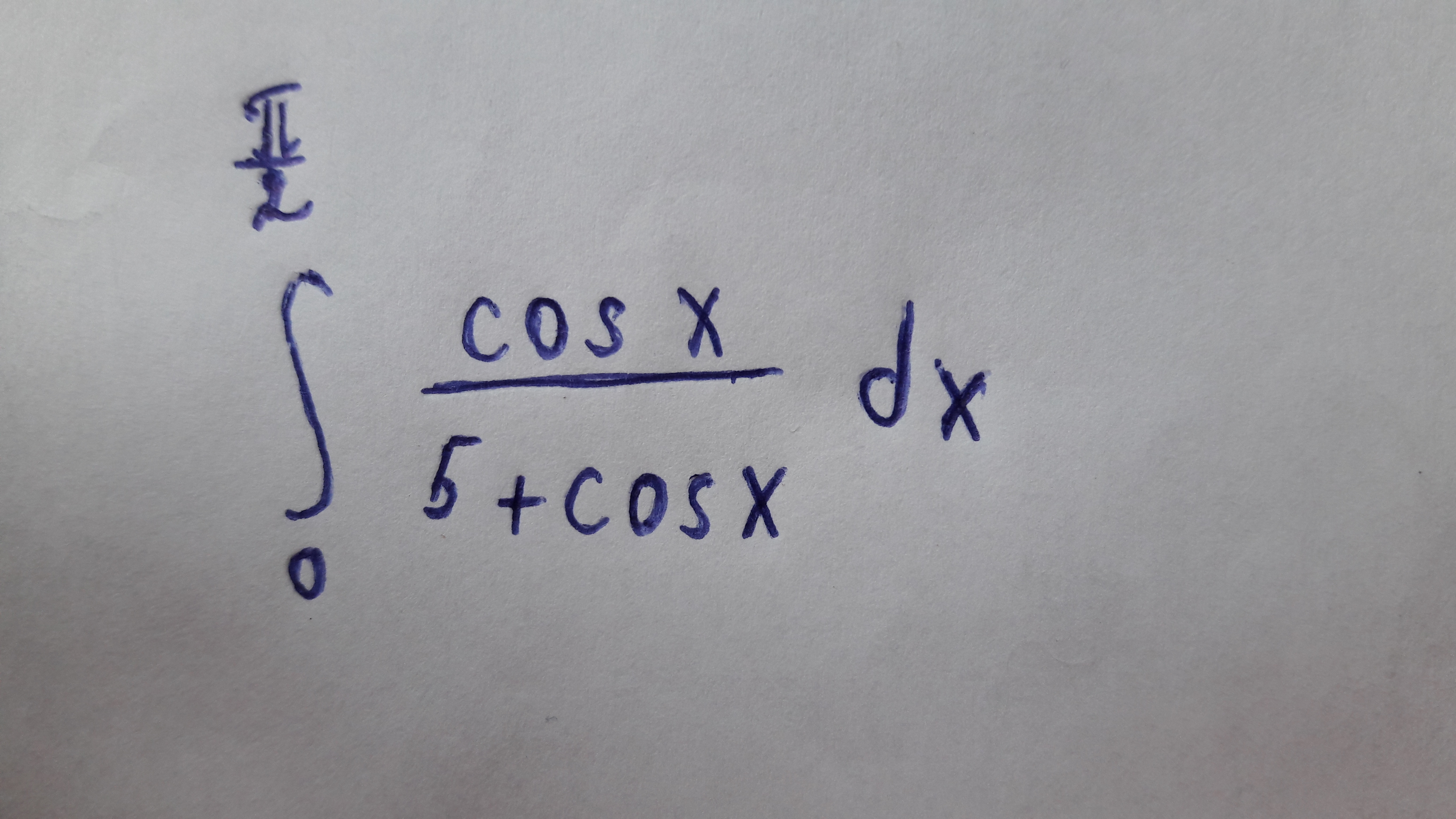

    question img

Ответы 12

  • Четвёртая строчка снизу, где после знака ' * ', - там в знаменателе не подправили (далее, кажется, тоже). К тому же при подведении под один знаменатель двух дробей не сходится первоначальная дробь.

    • Автор:

      luca57
    • 5 лет назад
    • 0
  • В интегралах ответы могут быть непохожими (особенно, когда получаются иррационально-дробно-смешанные числа). Поэтому "техничку" выполнить лучше самому, как бы странно здесь это ни выглядело. :)

    • Автор:

      bryancruz
    • 5 лет назад
    • 0
  • Благодарность модератору за оперативность.
  • А это точно формула Ньютона-Лейбница?

    • Автор:

      kayley
    • 5 лет назад
    • 0
  • Если вопрос мне, то "Да, конечно! Другой-то и нет".

    • Автор:

      rice
    • 5 лет назад
    • 0
  • 3B-2B-1=1: B=2 и тогда A= -5 еще тут недочет

    • Автор:

      aldo
    • 5 лет назад
    • 0
  • 2arctgt |_0^1=2(arctg1-arctg0)=2*П/4-0=П/2
  • Да, конечно.
  • Точно, "опечатка" на самом финише. Просьба модератору позволить исправить 2 на pi/2. Спасибо.

    • Автор:

      scruffy
    • 5 лет назад
    • 0
  • Исправлено, спасибо. Наверное, часть комментариев будет вводить посетителей в заблуждение... :)

    • Автор:

      kaleigh
    • 5 лет назад
    • 0
  • \int\limits^{\pi /2}_0 \, \frac{cosx}{5+cosx} dx =Q\\\\\int \frac{cosx}{5+cosx}dx=[\, t=tg \frac{x}{2}\; ,\; cosx= \frac{1-t^2}{1+t^2}\; ,\; dx= \frac{2\, dt}{1+t^2} \; ]=\\\\=\int \frac{2(1-t^2)dt}{(1+t^2)^2\cdot (5+\frac{1-t^2}{1+t^2})}=2\int \frac{(1-t^2)dt}{(1+t^2)(5+5t^2+1-t^2)} = 2\int \frac{(1-t^2)dt}{(1+t^2)(2t^2+3)\cdot 2} =\\\\=\int \frac{(1-t^2)dt}{(1+t^2)(2t^2+3)}\; \star\frac{1-t^2}{(t^2+1)(2t^2+3)} = \frac{At+B}{t^2+1} + \frac{Ct+D}{2t^2+3}1-t^2=(At+B)(2t^2+3)+(Ct+D)(t^2+1)\\\\t^3\; |\; 2A+C=0\; ,\; \; C=-2A\\\\t^2\; |\; 2B+D=-1\; \; ,\; \; D=-2B-1\\\\t^1\; |\; 3A+C=0\; ,\; \; 3A-2A=0\; ,\; A=0\\\\t^0\; |\; 3B+D=1\; ,\; \; 3B+(-2B-1)=1\; ,\; \; B=2\\\\D=-1-4=-5\; ,\; \; C=0\\\\\star \; \; \int \frac{2dt}{t^2+1}+\int \frac{-5\, dt}{2t^2+3}=2arctgt-\frac{5\sqrt2}{2\sqrt3}arctg\frac{t\sqrt2}{\sqrt3}+C=\\\\=2arctgtg(tg\frac{x}{2})- \frac{5}{\sqrt6} arctg\frac{\sqrt2\, tg\frac{x}{2}}{\sqrt3} +C=\\\\=2\cdot \frac{x}{2}-\frac{5}{\sqrt6}arctg\frac{\sqrt2\, tg\frac{x}{2}}{\sqrt3}+C)\; ;Q=(x- \frac{5}{\sqrt6}arctg \frac{\sqrt2\, tg\frac{x}{2}}{\sqrt3})\Big |_0^{\pi /2}=\frac{\pi }{2}-\frac{5}{\sqrt6}arctg \frac{1\cdot \sqrt2}{\sqrt3})=\frac{\pi }{2}- \frac{5}{\sqrt6}\cdot  arctg\sqrt{\frac{2 }{3}}

    • Автор:

      ubaldo
    • 5 лет назад
    • 0
  • Посмотрите предложенное решение. Метод интегрирования - универсальная тригонометрическая подстановка (первые квадратные скобки), метод разложения на сумму дробей - метод неопределённых коэффициентов (вторые квадратные скобки). По возможности перепроверьте коэффициенты.Оформление не соблюдалось.
    answer img

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years