-
Помогите решить данное тригонометрическое уравнение!
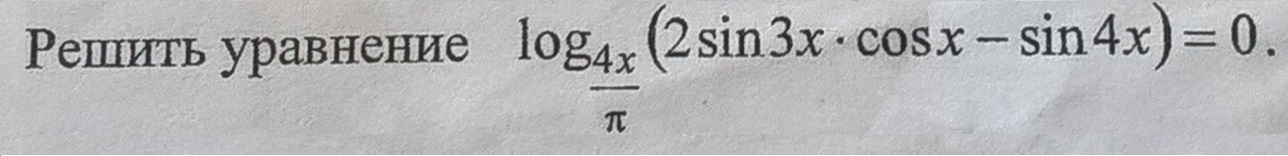
-
Предмет:
Математика -
Автор:
weineruxrr - 6 лет назад
-
Ответы 2
-
Заметим: sin4x = sin(x+3x) = sinx·cos3x + sin3x·cosxТогда 2sin3x·cosx - sin4x = 2sin3x·cosx - (sinx·cos3x + sin3x·cosx) = = sin3x·cosx - sinx·cos3x = sin(3x - x) = sin 2x.Поэтому исходное уравнение равносильно уравнению:
О.Д.З.:
Решаем уравнение: sin 2x = 1
"Разберемся" с О.Д.З.:
Теперь с учетом О.Д.З. решение уравнения есть:
Ответ:
, где n - неотрицательное целое число.

-
Автор:
miller - 6 лет назад
-
0
-
-
ОДЗ{4x/π>0⇒x>0{4x/π≠1⇒x≠π/4{2sin3x*cosx-sin4x>02sin3xcosx-sin(3x+x)>02sin3xcosx-sin3xcosx-sinxcos3x>0sin3xcosx-sinxcos3x>0sin(3x-x)>0sin2x>02πk<2x<π+2πkπk<x<π/2+πk,k∈zx∈(πk;π/4+2πk) U(π/4+2πk;π/2+πk),k∈z---------------------log(4x/π)sin2x=0sin2x=12x=π/2+2πkx=π/4+πk +ОДЗx=5π/4+2πk,k∈z

-
Автор:
simonschultz - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
2cosx=1-2(cos x)^2-sqrt3*sin(2x)
я так понимаю что надо решать методом доп аргумента но что то не сходиться. -
ПОМОГИТЕ ПОЖАЛУЙСТА )
Сложноподчинённое предложение. Главное и придаточное. Разберите
предложение: Мы учимся в колледже, чтобы получить профессиональные
знания и умения-
Предмет:
Русский язык -
Автор:
kendrick - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
1)признак творческой деятельности,отличающий её от трудовой-
1)удовлетворение потребностей людей
2)получение нового звания
3)наличие целеполагания
4)планируемость результата
2)Австралийский абориген обращается к идолу с заклянаниями.Этот пример иллюстрирует общение между
1)реальными суъектами
2)воображаемыми партнерами
3)реальным субъектом и иллюзорным партнёром
4)реальным субъектом и воображаемым партнёром-
Предмет:
Обществознание -
Автор:
codi - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Смесь пентагидрата сульфата меди и гептагидрата сульфата железа (II) массой 1,202 г растворили в воде и к полученному раствору добавили избыток раствора хлорида бария. Масса осадка составила 1,085 г. Найдите массовые доли компонентов в исходной смеси.
How much to ban the user?
1 hour
1 day
100 years
