-
Пусть f(0)=0, f(1)=3/2, f(n)=5/2f(n-1)-f(n-2), для n>=2. Вычислите значение бесконечной суммы 1/f(2^0)+1/f(2^1)+1/f(2^2)+...
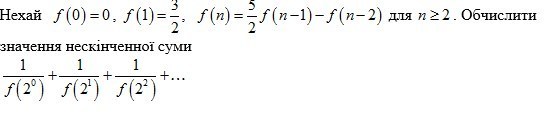
-
Предмет:
Математика -
Автор:
luke6cpx - 6 лет назад
-
Ответы 1
-
Попробуем найти решение рекуррентного соотношения f(n + 2) = 5/2 * f(n + 1) - f(n)в виде f(n) = a^n.a^(n + 2) = 5/2 a^(n + 1) - a^nСокращаем на a^n: a^2 = 5/2 a - 12a^2 - 5a + 2 = 0a = 2 или a = 1/2Заметим, что если f(n) и g(n) - решения, то и a f(n) + b g(n) - тоже решение. Воспользуемся этим, чтобы подобрать решение, удовлетворяющее начальным условиям.f(n) = a * 2^n + b * 2^(-n)f(0) = a + b = 0f(1) = 2a + b/2 = 3/2a = 1, b = -1Окончательно f(n) = 2^n - 2^(-n).Осталось вычислить сумму.
Ответ. 1
-
Автор:
mckenziegwom - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- докажите, что если: 1) 2 < a < 3, то 1/а-2 > 1; 2) -3 < а < -1 , то 1/а+1 < -1/2
-
Лодка плыли по течению 0,8 и против течения 0,3 часа .Собственная скорость лодки 3,8 км /ч, а скорость течения 1,3 км /ч. Какой путь пропала лодка за это время????
-
Предмет:
Математика -
Автор:
laineywoodard - 6 лет назад
-
Ответов:
6 -
Смотреть
-
-
записати число 961 трьома цифрами: 1, 2, 3
-
Предмет:
Математика -
Автор:
thunder thighs5sfn - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
за 9 м полотна и 8,5 сатина уплачено 2844 руб. Сколько уплачено за ткань каждого вида если 1 м полотна на 25% дороже 1 м Сатина
-
Предмет:
Математика -
Автор:
fifir2qf - 6 лет назад
-
Ответов:
7 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
