Задать вопрос Регистрация
Помочь другим

  • Как решить?
    Когда приводишь все к степени с основанием 3, остаются как степенная, так и показательная функции.
    Возможно, есть другие пути решения?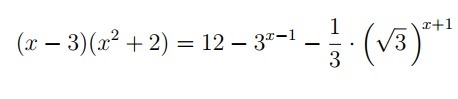

    question img

Ответы 1

  • Левая часть (x - 3)(x^2 + 2) имеет 1 корень x = 3.Правая часть 12-3^{x-1}- \frac{1}{3}*( \sqrt{3} )^{x+1}=12-3^{x-1}- \frac{ \sqrt{3} }{3} *( \sqrt{3} )^xЗамена t=( \sqrt{3} )^{x-1}\ \textgreater \ 0 при любом x.12-3^{x-1}- ( \sqrt{3} )^{x-1}=-t^2-t+12=-(t-3)(t+4)Правая часть имеет единственный корень при t=( \sqrt{3} )^{x-1}==3^{(x-1)/2}=3; \frac{x-1}{2}=1;x=3Таким образом, единственный корень: x = 3

    • Автор:

      rosalia
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years