Задать вопрос Регистрация
Помочь другим

  • Помогите кто знает как решать неравенства - огэ? Пожалуйста с обьяснением

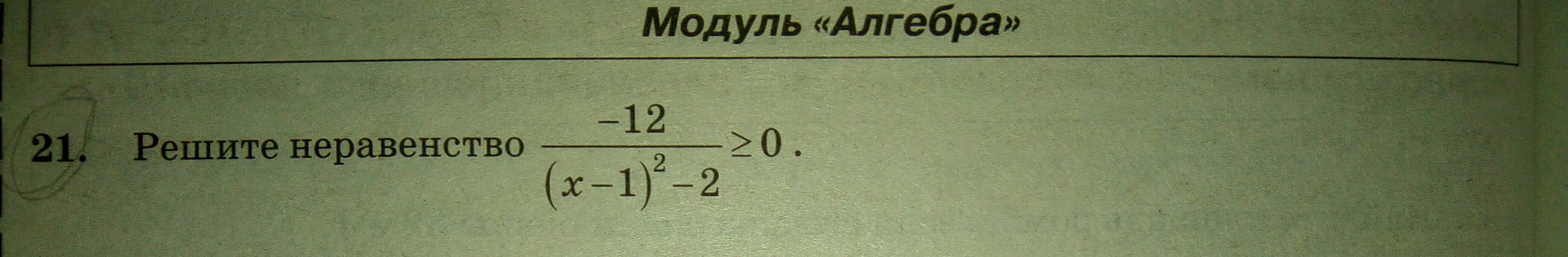
    question img

Ответы 2

  • Спасибо огромное

    • Автор:

      jackbftw
    • 5 лет назад
    • 0
  • На данный момент числитель не важен. Берем только знаменатель (x-1)^{2} -2\ \textgreater \ 0 (т.к. выражение стоит в знаменателе и не может быть равно нулю)Раскрываем по формуле x^{2}-2x+1 -2\ \textgreater \ 0 Приводим подобные слагаемыеx^{2}-2x-1 \ \textgreater \ 0Теперь нам надо ввести функцию и найти ее нулиf(x)=x^{2}-2x-1Чтобы найти нули функции ее надо приравнять к нулюx^{2}-2x-1= 0Теперь решаем уравнение, я решаю через теорему Виета \left \{ {{ x_{1}+ x_{2} =2 } \atop { x_{1} * x_{2} =1}} ight. x_{1} =1 x_{2} =1Мы нашли нули функции, теперь раскладываем на множители (x-1)^{2} \ \textgreater \ 0Строим прямую, отмечаем точку 1. Далее определяем знак на крайнем правом промежуткеf(2)=4-4+1=1f(2)\ \textgreater \ 0 (поэтому будет знак +)Смотрим, что точка 1 в неравенстве (x-1)^{2} \ \textgreater \ 0 встречается 2 раза, 2 четное число, значит переходя через точку 1, знак не изменяется.Тогда в ответ мы запишем все числа кроме 1 (там прокол)Ответ: x ∈ (-∞;1)∪(1;+∞)Надеюсь помогла, отметь это как лучший ответ) 

    • Автор:

      ottoknapp
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years