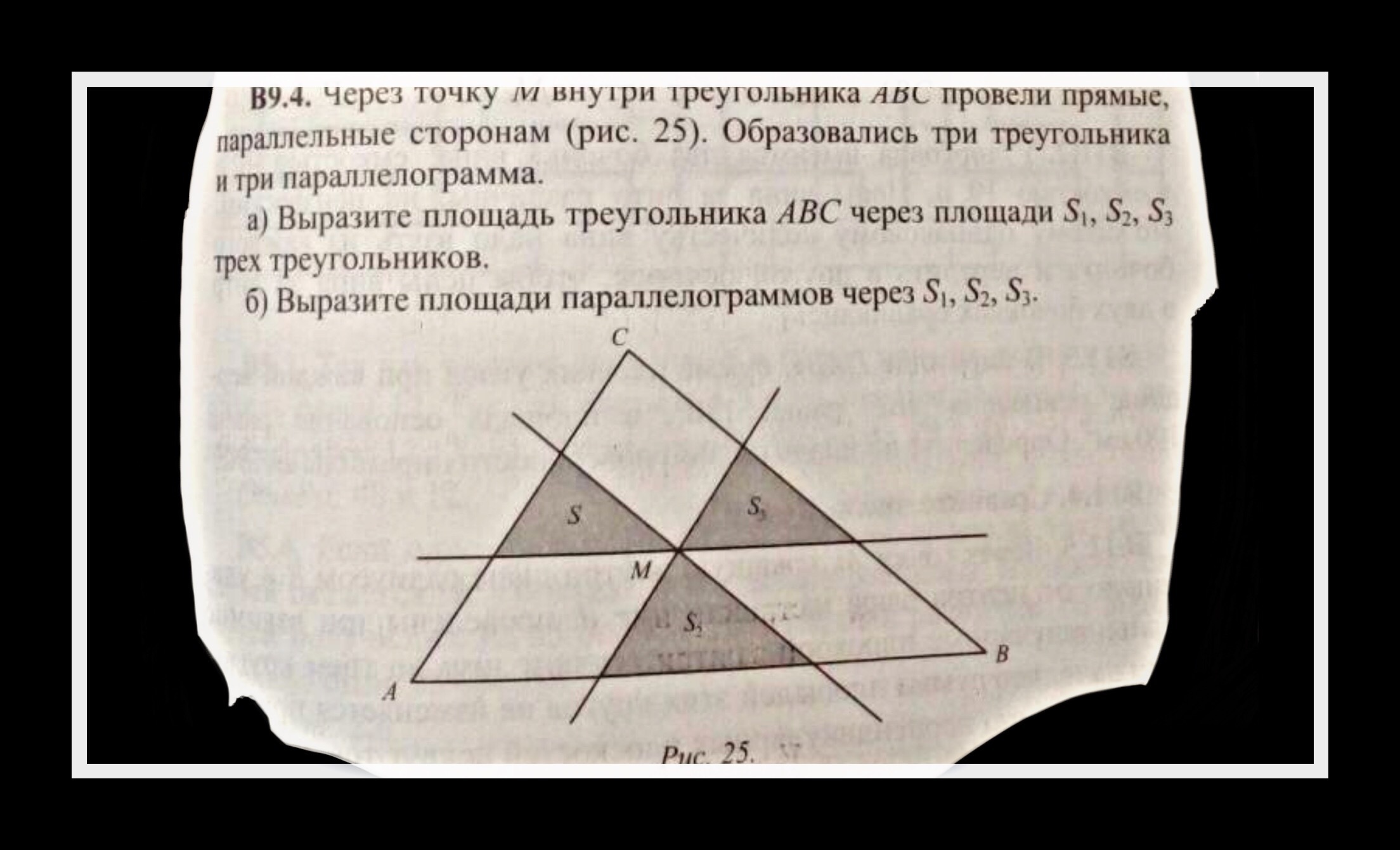
Через точку М внутри треугольника ABC провели прямые

Ответы 1

а) Все треуголники с площадями S1, S2, S3 подобны и подобны треугольнику АВС.Значит, их площади соотносятя как квадарты соответствующих сторон.Пусть стороны треугольников с площадями S1, S2, S3, параллельные стороне АВ равны a1, a2, a3 соответственно. ТогдаАВ=a1+a2+a3.Для каждого заштрихованного треугольника получаем соотношение: $\frac{S_i}{S_{ABC}} = (\frac{a_i}{a_1+a_2+a_3})^2; \sqrt{\frac{S_i}{S_{ABC}}} = \frac{a_i}{a_1+a_2+a_3}.$ $\sqrt{\frac{S_1}{S_{ABC}}} +\sqrt{\frac{S_2}{S_{ABC}}}+ \sqrt{\frac{S_3}{S_{ABC}}} = \frac{a_1+a_2+a_3}{a_1+a_2+a_3}=1,$ $\sqrt{S_{ABC}}=\sqrt{S_{1}}+\sqrt{S_{2}}+\sqrt{S_{3}};$ ${S_{ABC}}=(\sqrt{S_{1}}+\sqrt{S_{2}}+\sqrt{S_{3}})^2$ б) Рассмотрим параллелограмм при вершине А.Его площадь равна произведению стороны a1 на высоту треугольника с площадью S2. Получаем: $S_A=a_1*( \frac{S_2}{ \frac{1}{2}a_2 } )=2S_2* \frac{a_1}{a_2} =2S_2* \sqrt{ \frac{S_1}{S_2} } =2 \sqrt{S_1S_2} .$ Аналогично, $S_B=2 \sqrt{S_2S_3}; S_C=2 \sqrt{S_1S_3}$
- Автор:
  rolandrichmond
- 6 лет назад
- 0
Добавить свой ответ

Еще вопросы