Постройте гра­фик функ­ции
{3x-3.5 при x<2
y={-3x+8.5 при 2≤x≤3
{3.5x-11 при x>3
и определите, при каких зна­че­ни­ях m пря­мая y = m имеет с гра­фи­ком ровно две общие точки.

Ответ:

m=-0,5, m=2,5

Пошаговое объяснение:

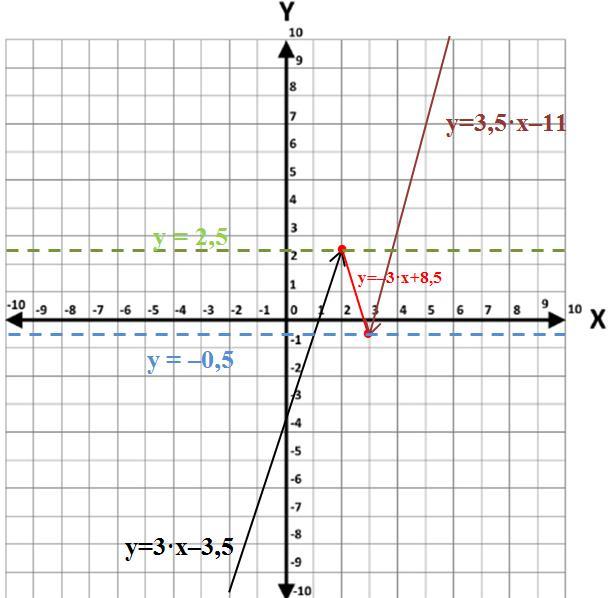
График кусочно-линейной функции (см. рисунок)

\displaystyle y=\left \{ \begin{array}{ccc} 3\cdot x-3,5, \;\; x<2 \\-3 \cdot x+8,5, \;\; 2\leq x \leq 3 \\3,5\cdot x-11, \;\; x>3 \end{array}\right

состоит из двух лучей и отрезка.  

y=m - это прямая, параллельная оси Ох. Поэтому:

а) при m<-0,5 прямая y=m пересекает только луч прямой y=3·x-3,5, то есть только одна общая точка;

б) при -0,5<m<2,5 прямая y=m пересекает луч прямой y=3·x-3,5, отрезок прямой y=-3·x+8,5 и луч прямой y=3,5·x-11, то есть три общих точек;

в) при m>2,5 прямая y=m пересекает только луч прямой y=3,5·x-11, то есть только одна общая точка.

Ответом будут (заштрихованные прямые) только :  m= -0,5 и m =2,5.