-
Решить неопределенный интеграл
Объяснить как внесли корень из икс под знак дифференциала!
Пропишите пожалуйста подробно как вы внесли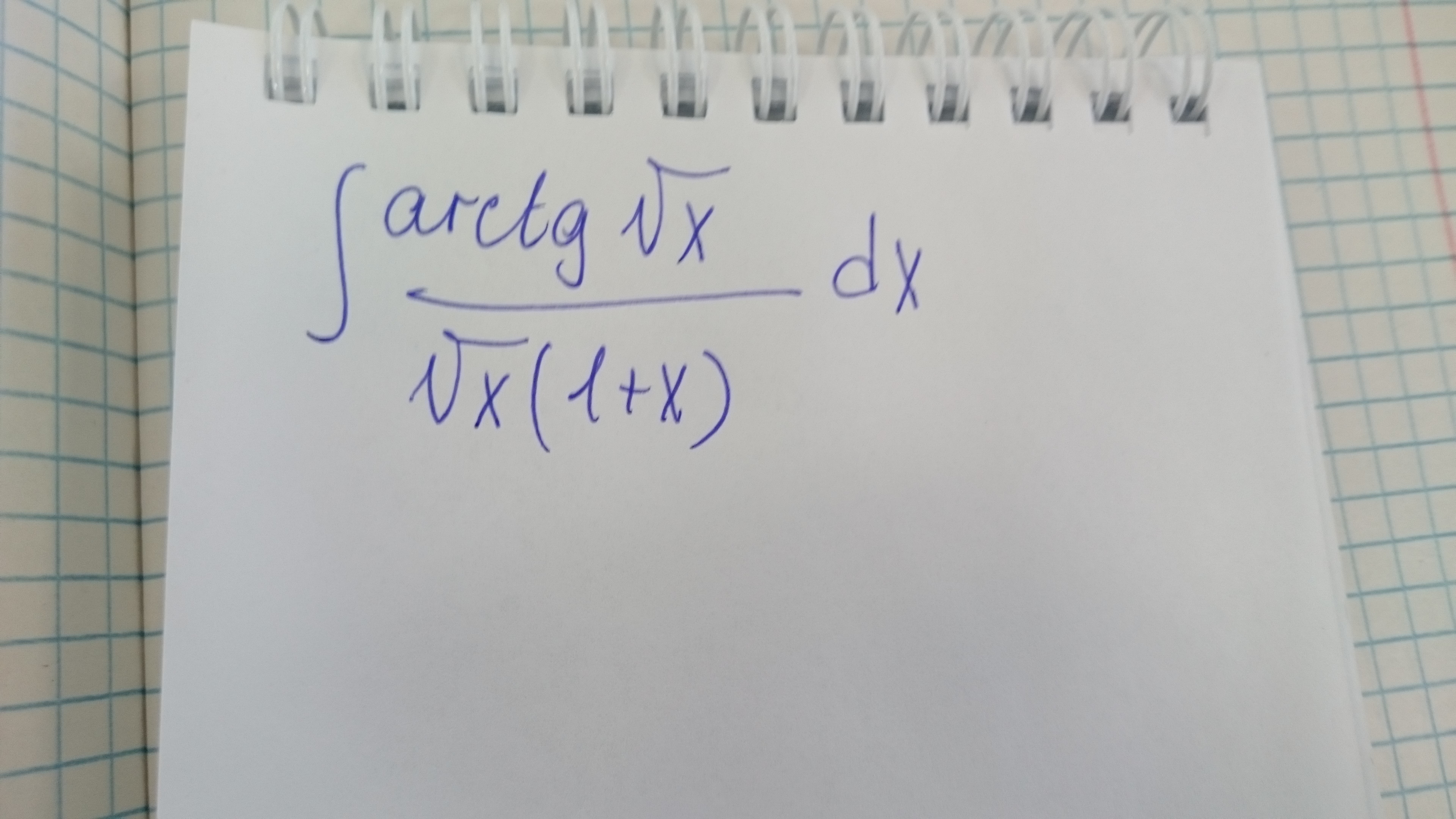
-
Предмет:
Математика -
Автор:
tatendqu - 6 лет назад
-
Ответы 2
-
спасибо большое!
-
Автор:
león82 - 6 лет назад
-
0
-
-
Рассмотрите такой вариант:в данном интеграле подводить под знак дифференциала можно дважды: сначала 1/√х, затем выражение 1/(1+х). Первое подведение [dx/√x=2d(√x)], о котором вопрос, алгебраически можно описать так (все обозначения условны, используются для пояснения):
Проще говоря, подведение под знак дифференциала - операция взятия производной, при условии, что будет домножение на коэффициент в целях сохранения равенства.Таким образом, выложенный интеграл решится примерно так:
-
Автор:
nicolás26 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Как называется правило когда ты написал Е, а не И в слове 3 скл
А то я написала не СинИ, а СинЕ, а эо 3 скл)))
Или такого правила нет?
-
Предмет:
Русский язык -
Автор:
larson - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Помогите ,пожалуйста
Составить предложения на тему "что ты должен и не должен делать для своего района " на английский с переводом )))
Даю 20 баллов!-
Предмет:
Английский язык -
Автор:
magdalena - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
переведите слово Hot и Noisy
-
Предмет:
Английский язык -
Автор:
parker78 - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
Тіло вільно падає з висоти 45 м. Чому дорцвнює швидкість тіла біля поверхні землі?
-
Предмет:
Физика -
Автор:
lorenzoeya9 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
