Задать вопрос Регистрация
Помочь другим

  • найти производные функций, высшая математика

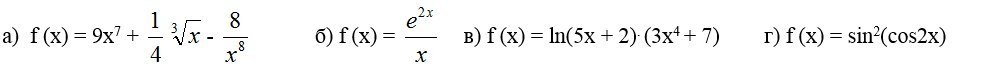
    question img

Ответы 1

  • а) f(x)= 9x^7+ \frac{1}{4} \sqrt[3]{x} - \frac{8}{x^8}=9x^7+ \frac{1}{4} x^{ \frac{1}{3} } - 8x^{-8} \\ \\ f'(x)= 9*7x^6+ \frac{1}{4} * \frac{1}{3} x^{- \frac{2}{3}} - 8*(-8)x^{-9}= \\ \\ =63x^6 + \frac{1}{12 \sqrt[3]{x^2} } + \frac{64}{x^9} б)f(x)= \frac{e^{2x}}{x} \\ \\ f'(x)= \frac{(e^{2x})'*x-e^{2x}*x'}{x^2} = \frac{2e^{2x}x-e^{2x}}{x^2} = \frac{e^{2x}}{x^2}(2x-1)в)f(x)= ln(5x + 2)*(3x^4+7) \\ \\ f'(x)=(ln(5x+2))'*(3x^4+7)+ln(5x+2)*(3x^4+7)'= \\ \\ = \frac{5(3x^4+7)}{5x+2} +ln(5x+2)*12x^3г)f(x) = sin²(cos2x)f'(x) = 2sin(cos2x)*(cos2x)' = 2sin(cos2x)*(-sin2x*(2x)') =      = -4sin (cos2x)*sin2x

    • Автор:

      josué71
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years