-
Логарифмические уравнения! Помогите с двумя заданиями
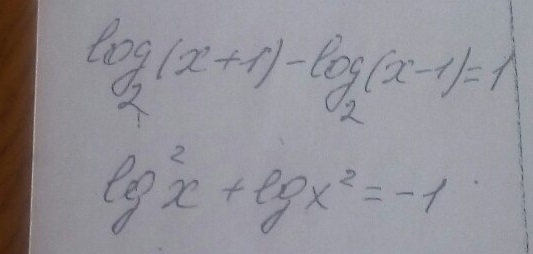
-
Предмет:
Математика -
Автор:
grant6 - 6 лет назад
-
Ответы 2
-
спасибо. я домой приду - проверю и оценю
-
Автор:
gooset1uk - 6 лет назад
-
0
-
-
1)
ОДЗ: х+1>0 и х-1>0; х>-1 и х>1. Следовательно, х>1.Разность логарифмов равна логарифму частного, т.е.
Дробь равна нулю, если числитель равен нулю, а знаменатель в ноль не обращается:-х+3=0 и х-1≠0х=3 и х≠1.Ответ: х=3.2)
ОДЗ: х>0Используя свойство логарифма от степени, уравнение запишем в виде
Ответ : х=1/10.
-
Автор:
loveymathews - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Знайдіть кілкість сторін правильного многокутника якщо його центральний кут дарівнює 60°
-
Решить уравнение с подробным объяснением.
(x^2 + 1/x^2) + (x + 1/x)=0-
Предмет:
Математика -
Автор:
katherineroberts - 6 лет назад
-
Ответов:
5 -
Смотреть
-
-
Сделайте морфологических разбор местоимения:
Этого.-
Предмет:
Русский язык -
Автор:
abdullah20 - 6 лет назад
-
Ответов:
5 -
Смотреть
-
-
краткое содержание щелкунчика и мышиного короля
-
Предмет:
Литература -
Автор:
pasha84 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
