-
для случайной величины распределенной по нормальному закону известно что М (Х) =5 D(Х) =4. Записать плотность вероятности f(x) и найти P(3<X<7)
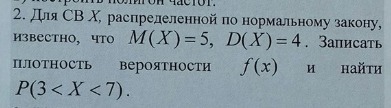
-
Предмет:
Математика -
Автор:
jeremiahzxg0 - 6 лет назад
-
Ответы 4
-
Кажись там ошибка в записи плотности распределения вероятностей. У вас 4√2, а должно быть 2√2, и в знаменателе не 5, а 2•2^2=8
-
Автор:
killianbass - 6 лет назад
-
0
-
-
действительно! спасибо!
-
Автор:
ellis - 6 лет назад
-
0
-
-
шаловливые пальчики не ту кнопочку нажали...
-
Автор:
terrell72 - 6 лет назад
-
0
-
-
Случайная величина х распределена нормально с математическим ожиданием M(x)=5 и математической дисперсией D(x)=4, следовательно m=5 и σ^2=4 ⇒ σ=2формула нахождения плотности распределения вероятностей имеет вид(σ будем писать через α, т.к. возможности вставить σ у меня нет)
тогда плотность распределения вероятностей f(x), будет равна
вероятность того, что случайная величина x, примет значения принадлежащие интервалу (a;b) вычисляются по формуле
(по-прежнему α это σ, а F это Φ - ну таковы тут возможности. просто когда будете переписывать не забывайте этого нашего вынужденного допущения)
ты же помнишь, функция F(x) является четной ((F(-x)=-F(x))по таблице значений функции Лапласа находим значения F(1)=0,3413следовательно вероятность будет равна 0,3413+0,3413=0,6826вот, пожалуй, и всё!
-
Автор:
jackbftw - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Как найти определяемое слово и причастный оборот в этом предложении: В глубине были видны не успевшие ещё дотянуться до поверхности воды круглые листки кувшинок.
-
Предмет:
Русский язык -
Автор:
hayliecy0k - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Как природные условия повлияли на занятия жителей Вавилонии
ПОМОГИТЕ ПОЖАЛУЙСТА!!!-
Предмет:
История -
Автор:
speedy0fdi - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Как будет "Друзья навсегда <3" ?)
-
Предмет:
Английский язык -
Автор:
giannalong - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- Дайте характеристику личности Цезаря и его государственной деятельности. Какие поступки Цезаря вы оцениваете положительно, а какие – нет?
How much to ban the user?
1 hour
1 day
100 years
