Найти частное решение (частный интеграл) дифференциального уравнения: y'-xy=2x^3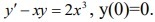

Найти частное решение (частный интеграл) дифференциального уравнения:
y'-xy=2x^3
- Предмет:
  Математика
- Автор:
  friscodoyle
- 5 лет назад

Ответы 1

ИСПОЛЬЗОВАН МЕТОД ЛАГРАНЖА.Найдем сначала общее решение соответствующего однородного уравнения $y'-xy=0$ - дифференциальное уравнение с разделяющимися переменными. $\displaystyle \frac{dy}{dx} =xy~~~\Rightarrow~~ \frac{dy}{y} =xdx~~~\Rightarrow~~~ \ln|y|= \frac{x^2}{2}+C$ $y=Ce^{\frac{x^2}{2} }$ - общее решение однородного уравненияПримем $C=C(x)$ , тогда $y=C(x)e^{\frac{x^2}{2} }$ . По правилу дифференцирования произведения: $y'=C'(x)e^{\frac{x^2}{2} }+xC(x)e^{\frac{x^2}{2} }$ Подставим данные в исходное уравнение: $C'(x)e^{\frac{x^2}{2} }+xC(x)e^{\frac{x^2}{2} }-xC(x)e^{\frac{x^2}{2} }=2x^3\\ C'(x)e^{\frac{x^2}{2} }=2x^3$ Получили дифференциальное уравнение с разделяющимися переменными $C(x)=\displaystyle \int 2x^3e^{-\frac{x^2}{2} }dx= \bigg\{u=x^2;~~ 2xdx=du\bigg\}= \frac{1}{2} \int ue^{- \frac{u}{2} }du=\\ \\ \\ = \frac{1}{2} \bigg(-2ue^{- \frac{u}{2} }+2\int e^{- \frac{u}{2} }du\bigg)=-2x^2e^{- \frac{x^2}{2} }-4e^{- \frac{x^2}{2} }+C_1$ Общее решение: $y=\bigg(-2x^2e^{- \frac{x^2}{2} }-4e^{- \frac{x^2}{2} }+C_1\bigg)e^{ \frac{x^2}{2} }=C_1e^{ \frac{x^2}{2} }-2x^2-4$ Найдем частное решение, подставляя начальные условия : $0=C_1e^{ \frac{0^2}{2} }-2\cdot0^2-4\\ C_1-4=0~~~\Rightarrow~~~ C_1=4$ $\boxed{y=4e^{ \frac{x^2}{2} }-2x^2-4}$ -ЧАСТНОЕ РЕШЕНИЕ.
- Автор:
  paul86
- 5 лет назад
- 0
Добавить свой ответ