Задать вопрос Регистрация
Помочь другим

  • Заданы математическое ожидание a и среднее квадратич-
    ное отклонение σ нормально распределенной случайной величины X . На-
    писать плотность распределения вероятностей . Найти вероятность того, что X примет значение из интервала
    (α,β)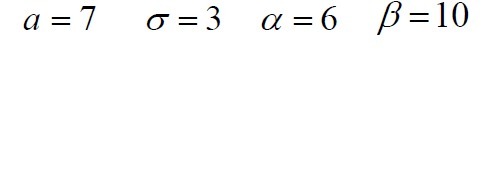

    question img

Ответы 1

  • Непрерывная случайная величина X, распределённая по нормальному закону, имеет функцию плотности:f(x)= \frac{1}{\sigma \sqrt{2 \pi } } e^{- \frac{(x-a)^2}{2\sigma ^2}}} В нашем случае: а=7, σ=3f(x)= \frac{1}{3 \sqrt{2 \pi } } e^{- \frac{(x-7)^2}{2*3 ^2}}= \frac{1}{3 \sqrt{2 \pi } } e^{- \frac{(x-7)^2}{18}} \\ \\ Вероятность попадания Х в интервал (α,β):P( \alpha \ \textless \ X\ \textless \ \beta )=\Phi ( \frac{ \beta -a}{\sigma} )-\Phi ( \frac{ \alpha -a}{\sigma} ) Где Ф(x) - функция Лапласа  (табличное значение)\frac{ \beta -a}{\sigma} =\frac{ 10-7}{3} =1 \\ \\ \frac{ \alpha -a}{\sigma} =\frac{ 6-7}{3} =-0,33Функция Лапласа нечетная, значит: Ф(-x)=-Ф(х), поэтомуP( 6 \ \textless \ X \ \textless \ 10 )=\Phi ( 1 )-\Phi (-0,33 ) =\Phi ( 1 )+\Phi (0,33 ) = \\ \\ =0.3413+0.129 3=0.4706 OTBET: \ f(x)= \frac{1}{3 \sqrt{2 \pi } } e^{- \frac{(x-7)^2}{18}} \\ \\ P( 6 \ \textless \ X \ \textless \ 10 )=0.4706
    answer img

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years