-
Используя метод математической индукции, докажите следующие утверждения:
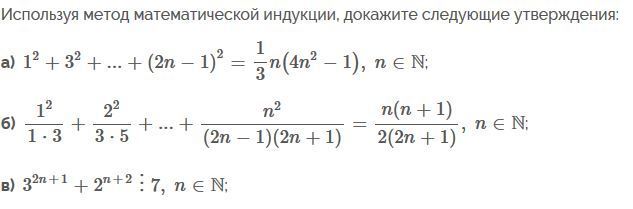
-
Предмет:
Математика -
Автор:
trevonhood - 6 лет назад
-
Ответы 3
-
что именно вам не понятно в трельем?
-
Автор:
alyvia0wr3 - 6 лет назад
-
0
-
-
1) Во-первых, проверим, является ли предложение истинным.1^2 = (1/3*1)(4*4*1 - 1) = 1/3 * 3 = 1, следовательно является.Во-вторых, проверим, остается ли.3^2 = 9; (1/3)*2(16-1) = 9+1(первое) следовательно остается, следовательно - правильно2) Во-первых, проверим, является ли предложение истинным.(1^2)/(1*3) = (1*(1+1))/(2*(2*1 +1)) = 2/6 =1/3, следовательно является.Во-вторых, проверим, остается ли.(2^2)/(3*5) = 4/15; (2*(2+1))/(2*(2*2 + 1)) = 4/15 + 1/3 (первое) = 6/10, следовательно является3) Не понятна распечатка, следовательно не могу выполнить задание
-
Автор:
macey4mvt - 6 лет назад
-
0
-
-
1) Для n=1 верно.Пусть верно для Н. Докажем, что верно для Н+1Сумму обозначим С(Н).C(H)=4H^3/3-H/3 С(Н+1)=1/3*(Н)*(4Н*Н-1)+(2Н+1)^2=4H^3/3-H/3+4H^2+4H+1=4/3*(H^3+3H^2+3H+1)-(H+1)/3=4(H+1)^3/3-(H+1)/3, что и требуется.2) Для n=1 верно.Пусть верно для Н. Докажем, что верно для Н+1Сумму обозначим С(Н) С(Н+1)=(H^2+H)/(2*(2H+1))+H*H/((2H+1)*(2H+3))=((H+1)^2+(H+1)/(2*(2H+3)) последнее получается простыми преобразованиями и доказывает утверждение.3) Для n=1 верно.3^3+2^3=27+8 на 7 делится.Обозначим сумму С(Н) и пусть она на 7 делится.С(Н+1)=3^(2H+3)+2^(H+3)= 9*(3^(2H+1)+2^(H+1)*4/9)=9*(3^(2H+1)+2^(H+1)+2^(H+1)*2/9-2^(H+1))=9C(H)+2*2^(H+1)-9*2^(H+1)=9*C(H)-7*2^(H+1) на 7 делится, т..к. С(Н) на 7 делится по предположению индукции.
-
Автор:
moisésqyvm - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Выпишите словосочетания:дождь и ветер,холодная осень,сырая земля,весна наступила,холмистая местность,низкая сторожка,осенний парк,сухие ветки, я пришла, сверкают на солнце
-
Предмет:
Русский язык -
Автор:
jasper9 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- В треугольнике ABC сторона ab=12, угол А=60, С=80. построена окружность в центре точки B и касающаяся стороны AC. Найти площадь общей части круга и треугольника
- Когда было начало и конец постройки Большого Цирка в Риме
-
Дан угол падения 50° чему равен угол отражения , угол между падающим лучом и отражённым , уогл между зеркалом и падающим лучом
-
Предмет:
Физика -
Автор:
madysonnavarro - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
