-
Нужно решить тригонометрические уровнения (кроме первого)
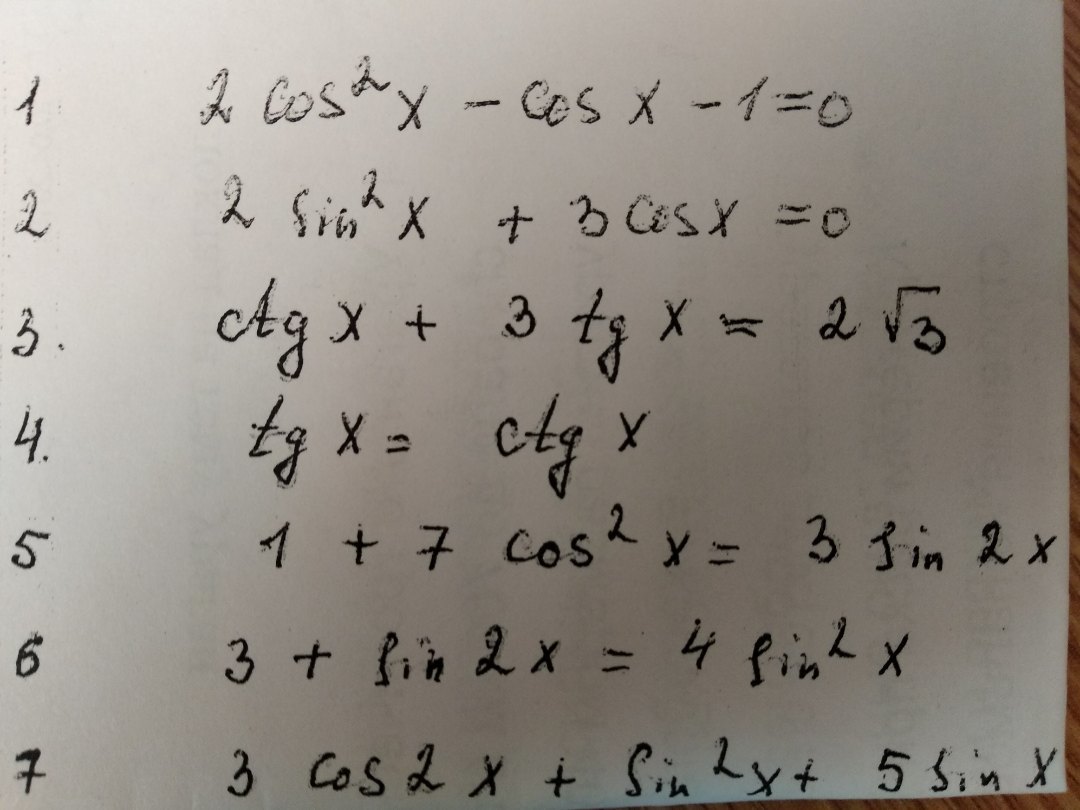
-
Предмет:
Математика -
Автор:
royceh26z - 6 лет назад
-
Ответы 1
-
2)
Пусть cosx = t
D = 9 - 4*2*(-2) = 25t1 = (3+5)/4 = 2t2 = (3-5)/4 = -1/2cosx = 2x= +- arccos2 + 2*pi*n, n€Zcosx = -1/2x = +- (pi - arccos1/2) + 2*pi*n, n€Z3) ctgx + 3tgx = 2 sqrt (3)1/tgx + tgx = 2sqrt (3)(tg^2x + 1)/tgx = 2sqrt (3)tg^x - 2sqrt (3)*tgx +1 =0Пусть tgx=tt^2-2sqrt (3)t+1 =0D = 12 - 4*1 = 8t1,2 = (2sqrt (3)+-2sqrt (2))/2x = arctg(sqrt (3)+sqrt (2)) + pi*n, n €Zx= arctg (sqrt (3)-sqrt (2)) + pi*n, n €Z4) tgx = ctgx tgx/ctgx = 1tg^2x = 1tgx=1tgx=-1x=pi/4 + pi*n, n €Zx= -pi/4 + pi*n, n €Z5 и 6 не уверен, как решать.
-
Автор:
graciexap1 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
в каком предложении оба выделенных слова пишутся слитно? Раскройте скобки и выпишите эти 2 слова.
1.) (И)так лирический герой Пастернака чувствует, что любовь помогает преодолеть суету и пошлость мира, и (По)тому вспоминает о погасшей когда-то искре любви с сожалением.
2.) (В)течение двадцати лет изъездил в Россию по всем направлениям , но всё(же) лучшего места чем отчий край, не нашёл.
3.) Исходя из представления о предопределенности можно (НА)перёд оправдать любой поступок человека, сколько(бы) отталкивающем или преступным он нам не казался.
4.) Теперь Чацкому да(же) не о чем поговорить с Софьей, но всё(равно) он любит её.
-
Предмет:
Русский язык -
Автор:
sebastian41 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Найдите производную y=(1/5x-10)^25
-
В равнобедренном треугольнике ABC с основанием АС проведена проведена биссектриса СК.Найдиье углы треугольника ABC,если угол AKC=60°
- Пожалуйста, помогите составить уравнение прямой проходящей через точки А( 1 ; 4 ) и B( -1 ; -2)
How much to ban the user?
1 hour
1 day
100 years
