-
Касательные в точках A и B к окружности с центром O пересекаются под углом 18°. Найдите угол AOB. Ответ дайте в градусах.
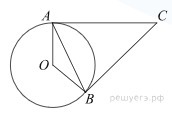
-
Предмет:
Математика -
Автор:
desmond - 6 лет назад
-
Ответы 4
-
180-18=162
-
Автор:
nelsonlloyd - 6 лет назад
-
0
-
-
?????
-
Автор:
lucyxhoh - 6 лет назад
-
0
-
-
<АО = 360°-90°-90°-18°=162°Ответ:162°
-
Автор:
dashawnmcmillan - 6 лет назад
-
0
-
-
∠ACB=18° так как касательные ⊥ радиусам в точке касания то ∠OAC=∠OBC=90°треугольники ОАС и ОВС прямоугольные у них катеты ОА=ОВ так как это радиусы и гипотенуза ОС общая⇒ОАС=ОВС по катету и гипотенузе⇒∠АСО=∠ВСО=18°/2=9°∠AOC=∠BOC=90°-9°=81°∠AOB=∠AOC+∠BOC=81+81=162°
-
Автор:
rocketfuel - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
какая методика обучения помогает двоечнику стать отличником
-
Предмет:
Другие предметы -
Автор:
mckennagarza - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Радиус основной усеченного конуса равны 15 см и 12 см, высота 4см. чему равна образующая конуса?
-
Предмет:
Математика -
Автор:
dots - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
часы показывают 11:00 какой угол между минутной и часовой стрелками
-
Предмет:
Алгебра -
Автор:
headlights - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
(6^3)4*6^5
-------------- =
(6^7)^2-
Предмет:
Математика -
Автор:
petie - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
