Задать вопрос Регистрация
Помочь другим

  • как решать такие штуки напишите пожалуйста подробно

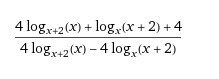
    question img

Ответы 1

  • Применяем формулу перехода к другому основанию:

    log_{a}b=\frac{log_{c}b}{log_{c}a}

    a>0, a ≠ 1, b>0, c>0, c≠1

    Тогда

    log_{x+2}x=\frac{1}{log_{x}(x+2)}

    Обозначим

    log_{x+2}x=t

    тогда

    log_{x}(x+2)=\frac{1}{t}

    \frac{4t+\frac{1}{t}+4}{4t-\frac{4}{t}}=\frac{4t^2+4t+1}{4t^2-4} =\frac{(2t+1)^2}{4\cdot(t^2-1)}

    \frac{(2t+1)^2}{4t^2-4} \ \textgreater \ 0 Применяем метод интервалов:__-__ (-1) ___+__ (-1/2) ________-__________  (1) _+__t < -1     или   (-1/2) < t < 1log_{x+2}x \ \textless \ -1 \\ log_{x+2} x \ \textless \ -1 \cdot log_{x+2}(x+2) \\ log_{x+2} x \ \textless \ log_{x+2}(x+2)^(-1) \\ log_{x+2} x \ \textless \ log_{x+2} \frac{1}{x+2} Применяем метод рационализации логарифмических неравенств:{(x+2-1)·(x-(1/x+2)) < 0{x>0, x≠1{x+2>0, x+2≠1(x+1)·(x^2+2x-1)/(x+2) < 0D=8x₁=-1-√2  или    x₂=-1+√2_+_ ( x₁) _-_ (-2) __+__ (-1) __-__ (x₂) _+__С учетом второго и третьего неравенств: (0; -1+√2) Аналогично решаем и второе неравенство

    • Автор:

      kaleb
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years