Задать вопрос Регистрация
Помочь другим

  • Помогите решить обе системы уравнений методом Крамера и Гаусса

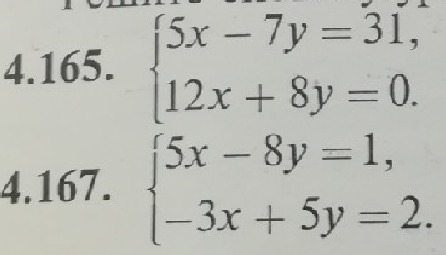
    question img

Ответы 1

  • Ответ:

    Пошаговое объяснение:

    4.165 Метод Крамера:

    \Delta=\left[\begin{array}{ccc}5&{-7}\\12&8\end{array}ight]=40+84=124\\\Delta_x=\left[\begin{array}{ccc}31&{-7}\\0&8\end{array}ight]=248\\\Delta_y=\left[\begin{array}{ccc}5&{31}\\12&0\end{array}ight]=-372\\x=\frac{\Delta_x}{\Delta}=\frac{248}{124}=2\\y=\frac{\Delta_y}{\Delta}=\frac{-372}{124}=-3

    Метод Гаусса:

    \left\{{{5x-7y=31}\atop{12x+8y=0}}ight.\\\left\{{{5x-7y=31}\atop{8y+\frac{12}{5}*7y=31*(-\frac{12}{5})}}ight.\\\left\{{{5x-7y=31}\atop{124y=-372}}ight.\\\left\{{{5x-7y=31}\atop{y=-3}}ight.\\\left\{{{5x+21=31}\atop{y=-3}}ight.\\\left\{{{x=2}\atop{y=-3}}ight.

    4.167 Метод Крамера:

    \Delta=\left[\begin{array}{ccc}5&{-8}\\-3&5\end{array}ight]=25-24=1\\\Delta_x=\left[\begin{array}{ccc}1&{-8}\\2&5\end{array}ight]=5+16=21\\\Delta_y=\left[\begin{array}{ccc}5&{1}\\-3&2\end{array}ight]=10+3=13\\x=\frac{\Delta_x}{\Delta}=21\\y=\frac{\Delta_y}{\Delta}=13

    Метод Гаусса:

    \left\{{{5x-8y=1}\atop{-3x+5y=2}}ight.\\\left\{{{5x-8y=1}\atop{5y-\frac{3}{5}*8y=2+\frac{3}{5}*1}}ight.\\\left\{{{5x-8y=1}\atop{y=13}}ight.\\\left\{{{5x-104=1}\atop{y=13}}ight.\\\left\{{{x=21}\atop{y=13}}ight.

    • Автор:

      fideltp3c
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years