Задать вопрос Регистрация
Помочь другим

  • Найти производные функций, можно только всё подробно, с объяснением

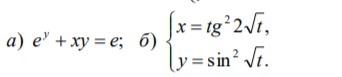
    question img

Ответы 1

  • 1)  Так как из заданного равенства выразить "у" невозможно, то найдём производную неявно заданной функции, учитывая, что "у" - функция, то есть у=у(х).

    e^{y}+xy=e\; \; \; \Rightarrow \; \; \; e^{y}+xy-e=0\\\\(e^{y})'+(xy)'-e'=0\\\\e^{y}\cdot y'+(x'y+xy')-0=0\\\\e^{y}\cdot y'+1\cdot y+x\cdot y'=0\\\\e^{y}\cdot y'+y+xy'=0\\\\y'\cdot (e^{y}+x)=-y\\\\y'=-\frac{y}{e^{y}+x}

    2)\; \; \left \{ {{x=tg^2\, 2\sqrt{t}} \atop {y=sin^2\sqrt{t}}} ight. \qquad y_{x}=\frac{y'_{t}}{x'_{t}}\\\\y'_{t}=2sin\sqrt{t}\cdot (sin\sqrt{t})'=2\, sin\sqrt{t}\cdot cos\sqrt{t}\cdot (\sqrt{t})'=sin(2\sqrt{t})\cdot \frac{1}{2\sqrt{t}}\; ;\\\\x'_{t}=2\, tg(2\sqrt{t})\cdot (tg(2\sqrt{t}))'=2\, tg(2\sqrt{t})\cdot \frac{1}{cos^2(2\sqrt{t})}\cdot (2\sqrt{t})'=\\\\=2\, tg(2\sqrt{t})\cdot \frac{1}{cos^2(2\sqrt{t})}\cdot \frac{2}{2\sqrt{t}}=\frac{2\, sin(2\sqrt{t})}{\sqrt{t}\, \cdot \, cos^3(2\sqrt{t})}

    y'_{x}=\frac{sin(2\sqrt{t})}{2\sqrt{t}}:\frac{2\, sin(2\sqrt{t})}{\sqrt{t}\, \cdot \, cos^3(2\sqrt{t})}=\frac{1}{4}\, cos^3(2\sqrt{t})

    • Автор:

      drake872
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years