-
Мат анализ
Под номером 2 и 3
Найти производную методом логарифмического дифференцирования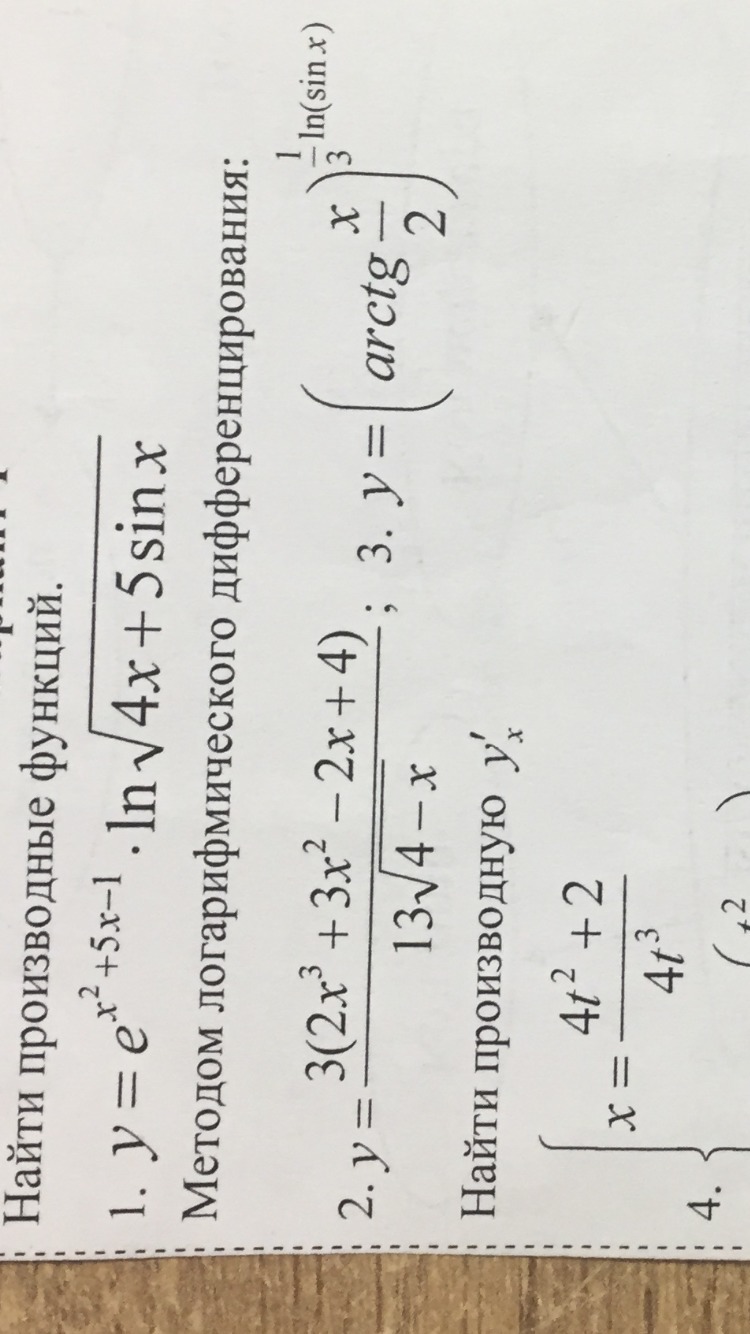
-
Предмет:
Математика -
Автор:
oliviamiller - 6 лет назад
-
Ответы 2
-
Решение выполнено без подставления исходного значения вместо у.

-
Автор:
blastgonzales - 6 лет назад
-
0
-
-

-
Автор:
goosecgsz - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Определите модуль равнодействующей силы (масштаб:1H)Фото прилагается!!ПОМОГИ!!!!!УМОЛЯЮЮЮ50 баллов!!!!!
-
Предмет:
Физика -
Автор:
pandorabradshaw - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
ПОМОГИТЕ СРОЧНО СОСТАВИТЬ ПРЕДЛОЖЕНИЯ С ДАННЫМИ СЛОВАМИ! visit, prefer(iVing), you can find..............in Moscow ( к примеру) , I find if important( useful,handy, comfortable,convenient....,
be founded by / in.....
go sightseeing
do/ see the sights lot
places of interest-
Предмет:
Английский язык -
Автор:
mario52 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
54 квадратных метров это сколько обычных см в масштабе 1:100?
СРОЧНО-
Предмет:
Математика -
Автор:
chesterengm - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
Пожалуйста, соедините по смыслу картинку и описание пути.
-
Предмет:
Немецкий язык -
Автор:
philip - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
