-
решите неравенство
x^2(1-x)
_______ [tex] \leqslant [/tex]
x^2-6x+9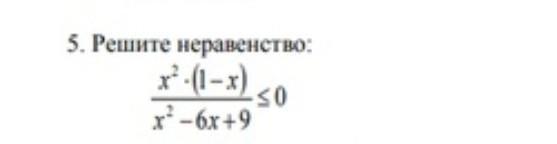
-
Предмет:
Математика -
Автор:
kimoraguerrero - 6 лет назад
-
Ответы 2
-
Благодарю!
-
Автор:
nibby - 6 лет назад
-
0
-
-
И так можно сразу метод интервалов, а можно немного упростить.
x² это всегда не отрицательное выражение, поэтому если оно равно нулю, то 0≤0 и это значение подходит, а если оно не равно нулю, то можно поделить и знак равенства не поменяется т.к. оно положительное. Получается:
В знаменателе выражение тоже не отрицательное, но оно ещё и в знаменателе поэтому оно строго больше нуля (всегда только положительно), поэтому мы просто домножаем на это выражение, запомнив, что оно не равняется нулю. Получается:
Можно сразу дать ответ.
Ответ: {0}∪[1;+∞)\{3}
или
x=0 и x∈[1;3)∪(3;+∞).
-
Автор:
raquel94 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Файл размером 9 Мбайт передаётся через некоторое соединение за 240 секунд. Определите размер файла (в Мбайт), который можно передать через это же соединение за 80 секунд. В ответе укажите одно число — размер файла в Мбайт. Единицы измерения писать не нужно
-
Предмет:
Информатика -
Автор:
denise - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Угол при вершине равнобедренного треугольника равен 120∘, а высота, проведенная к основанию, - 3√3 см. Найдите основание треугольника.
-
У посудину з водою опустили 3 циліндра однакового об'єму виготовлені зі сталі олова і свинця. На який циліндра діє більша сила Архемеда?
-
ДАЮ 60 БАЛЛОВ
Студент Василий живет в общежитии. Отделение банка, в котором он производит оплату за проживание, имеет всего две кассы, поэтому почти всегда длинная очередь к ним. Первая касса открывается в 8.00, вторая – в 8.05. Последний клиент будет принят в 20.00. Очередь единая, и очередной клиент обслуживается, как только освобождается одна из касс. На обслуживание одного клиента уходит ровно 10 минут. Василий приходит ровно в 8.00 и видит, сколько человек стоит перед ним. Требуется определить, сколько времени ему придется простоять в очереди, и вообще обслужат ли его сегодня.
Помогите пожалуйста очень срочно
Сделать в паскале и построить блок-схему-
Предмет:
Информатика -
Автор:
oliver15 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
