-
Докажите что при любых значениях переменной выполняется неравенство
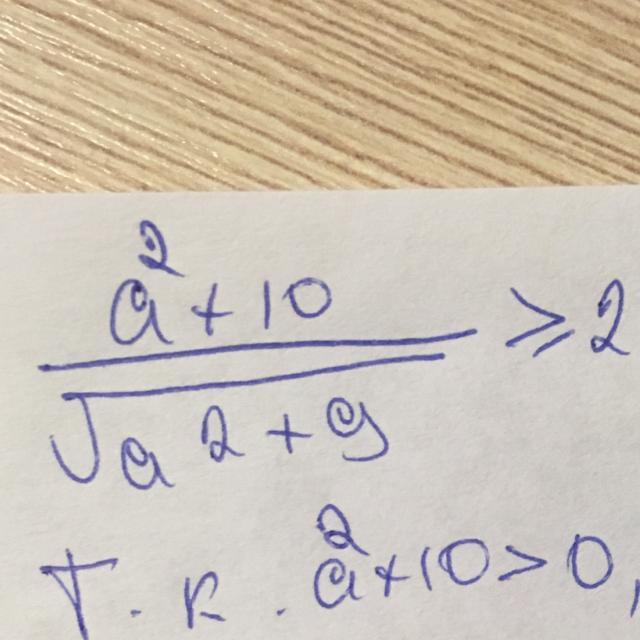
-
Предмет:
Математика -
Автор:
borja1ffx - 6 лет назад
-
Ответы 1
-
Наименьшее значение подкоренное выражение достигает при а=0, оно равно 9, а корень из 9 равен трем, в то время как в числителе получаем 10, но 10/3 больше 3, а, значит, и подавно больше двух.
Если же а не равное нулю, то (а²+10)/√(а²+9)=((а²+9)+1)/√(а²+9)=
√(а²+9)+1/√(а²+9), только что доказали, что при а=0, получаем самое маленькое значение дроби, а если взять любое другое число, положительное, или отрицательное, то квадрат этого числа увеличит подкоренное выражение, и корень будет больше трех, а значит, и двух, да еще добавка в виде положительной дроби
1/√(а²+9) только добавит положительное число. Поэтому исходное выражение в задачи не будет меньше двух.
-
Автор:
kaiden - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Туған елімізді суреттеп Қазақстан саяхатшылар көзіментақырыбындв эссе құрау
-
Предмет:
Қазақ тiлi -
Автор:
bo - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Написати твір (чому на вашу думку твір дістав назву не ,,Устина" не ,,Панночка", а саме Інститутка?)
-
Предмет:
Українська література -
Автор:
javion - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Ответе плз на вопросы по английскому дам 60 баллов.
-
Предмет:
Английский язык -
Автор:
leslybarton - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Помогите написать пж my marks at school
-
Предмет:
Английский язык -
Автор:
camiloxalh - 6 лет назад
-
Ответов:
0 -
Смотреть
-
