-
Вычислите площадь диагонального сечения правильной четырехугольной пирамиды если её высота равна 4 см а сторона основания равна 3 корень из 2 помогите пожалуйста, срочно!
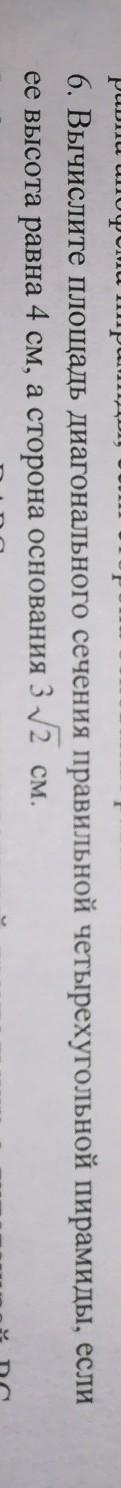
-
Предмет:
Математика -
Автор:
odiefze7 - 6 лет назад
-
Ответы 1
-
Для того чтобы вычислить площадь диагонального сечения правильной четырехугольной пирамиды, нам нужно знать длину диагонали основания пирамиды и высоту пирамиды.
1. Найдем длину диагонали основания: Диагональ основания правильной четырехугольной пирамиды (квадрата) равна диагонали квадрата и может быть найдена по теореме Пифагора: d^2 = a^2 + a^2, где d - диагональ, a - сторона квадрата. d^2 = (3√2)^2 + (3√2)^2 d^2 = 18 + 18 d^2 = 36 d = √36 = 2√2 (см).
2. Теперь мы можем найти площадь диагонального сечения пирамиды (треугольника), которое образуется высотой пирамиды, половиной диагонали основания и самой диагональю: S = (1/2)dh, где d - длина диагонали, h - высота пирамиды. S = (1/2)(2√2)(4) S = 4√2 (см^2).
Таким образом, площадь диагонального сечения правильной четырехугольной пирамиды равна 4√2 см^2.
-
Автор:
Queenmagic18 - 2 года назад
-
-1
-
-
Добавить свой ответ
-
Приведите факты современной жизни, которые подтверждают, что достижения греко-римской цивилизации используются нашими современниками.
Приведите 6 аргументов.
СРОЧНО-
Предмет:
Литература -
Автор:
totognqy - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Объем информационного сообщения, составленного из символов алфавита мощностью 64, по сравнению с объемом сообщения, составленного из символов алфавита мощностью 8
1) больше в 2 раза
2) меньше в 2 раза
3) больше в 3 раза
4) меньше в 3 раза
3. Файл объемом 700 Кбайт будет передан через канал связи с пропускной способностью 84 000 бит/с за
1) 120 с
2) 15 с
3) 30 мин
4) 2 мин
4. Если три сервера за 5 с обрабатывают 2 млн запросов, то шесть серверов за 10 с обработают
1) 4 млн запросов
2) 12 млн запросов
3) 6 млн запросов
4) 19 млн запросов
5. Информационный объем изображения, сохраненного в файле как 6-разрядный рисунок, по сравнению с этим же изображением, сохраненным как 8-цветный рисунок
1) меньше в 2 раза
2) больше в 2 раза
3) меньше в 4 раза
4) больше в 4 раза
6. Для хранения графического изображения, занимающего весь экран монитора с разрешением 2048 х 1536 пикселей и палитрой из 1024 цветов, потребуется
1) 20 Кбайт
2) 30 Мбайт
3) 21 Мбайт
4) 30 Кбайт
7. Если для хранения текста, сохраненного в восьмибитовой кодировке, требуется 60 Кбайт и на одной странице можно разместить 48 строк по 64 символа в каждой, то весь текст займет
1) 20 страниц
2) 98 страниц
3) 24 страницы
4) 20 страниц
8. Информационный объем фразы
Информация — движущая сила развития общества
сохраненной в кодировке Unicode, равен
1) 88 бит
2) 88 байт
3) 40 бит
4) 1600 байт
9. Для сохранения 1 мин видео на экране монитора с разрешением 800 х 600 и палитрой из 64 цветов требуется
1) 330 Кбайт
2) 330 Мбайт
3) 21 504 Кбайт
4) 21 Мбайт
ПОЖАЛУЙСТА С РЕШЕНИЕМ!!!!!!!-
Предмет:
Информатика -
Автор:
edgarhansen - 6 лет назад
-
Ответов:
5 -
Смотреть
-
- помогите построить график функции y-x^2+7x+2>>0
-
яку силу треба прикласти до тіла,що проходить шлях 2м ,щоб визнати роботу 400Дж?!!?!!?!?!
-
Предмет:
История -
Автор:
jessiepatrick - 6 лет назад
-
Ответов:
1 -
Смотреть
-
