-
С помощью дифференциала соответствующей функции вычислить приближенное значение данного выражения.
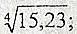
-
Предмет:
Математика -
Автор:
rosendorpj8 - 6 лет назад
-
Ответы 4
-
вы можете показать как это решать практически? не объясняя словами
-
Автор:
hansrowe - 6 лет назад
-
0
-
-
словами не очень понятно
-
Автор:
albertohale - 6 лет назад
-
0
-
-
показал практически.)
-
Автор:
lukeaskp - 6 лет назад
-
0
-
-
Корень энной степени из х+ дэльта х, приближенно равен корню энной степени из икс прибавить частное от дэльта икс деленное на произведение эн на корень ээной степени из икса в степени эн минус один. В Вашем случае эн равно 4. а 15.23 =16-0.77, здесь дэльта икс оказалась меньше нуля, значит, в формуле надо сменить плюс на минус
окончательно получим
≈(16)¹/⁴-(0.77)/((4*(16)³/⁴)=2-0.77/32=2-0.0240625=1.9759375
f(х+∆х) = f(x) + ду ≈ f(x) + f'(х)·дх.
f(x)-это корень четвертой степени из 16, он равен 2
дх-это -0.77, т.к. 15.23=16-0.77
f'(х)-это производная корня четвертой степени из икс, она равна 4*х³/⁴=4*2³/⁴=4*8=32
подставляем в формулу и получаем ответ.
2-0.77/32=2-0.0240625=1.9759375
-
Автор:
elliottjwsi - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Переведите текст на русский. Без переводчика, а то они всякую фигню переводят.
-
Предмет:
Английский язык -
Автор:
webster - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Замените изъявительные предложения глаголами в условном наклонении.Укажите число и род(если есть).
Мальчики спасли бездомную собачку.Я могу учиться на одни пятёрки.Пятиклассники поехали на экскурсию в Вильянди.Незнайка выступил на концерте.Внучка помогает бабушке печь праздничный пирог.Образец:
Я стану учителем-Я бы стал учителем.(ед.ч)-
Предмет:
Русский язык -
Автор:
paulahd6k - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
Особливості розвитку культури українських земель у XIII–XV ст. Тенденції
-
Предмет:
История -
Автор:
anselmophillips - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Кто убил Джейсона в романе портрет Дориана Грея
-
Предмет:
Литература -
Автор:
kaliholloway - 6 лет назад
-
Ответов:
1 -
Смотреть
-
