-
помогите решить дифференциальное уравнение (прикрепил скрин)
Заранее спасибо.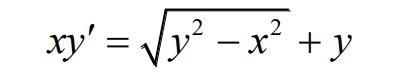
-
Предмет:
Математика -
Автор:
bridges - 6 лет назад
-
Ответы 1
-
Ответ:
Пошаговое объяснение:
xy'(x)=√(y(x)^2 -x^2) +y(x)
x•dy(x)/dx=√(-x^2 +y(x)^2) +y(x)
Возьмем y(x)=xv(x), тогда:
dy(x)/dx=x•dv(x)/dx +v(x)
x(x•dv(x)/dx +v(x)=√(-x^2 +x^2 •v(x)^2) +xv(x)
x(x•dv(x)/dx +v(x)=x(√(v(x)^2 -1) +v(x))
Находим для:
dv(x)/dx=(√(v(x)^2 -1))/x
Делим обе стороны на числитель правой стороны:
(dv(x)/dx)/√(v(x)^2 -1)=1/x
Теперь интегрируем обе стороны по отношению к х:
∫(dv(x)/dx)/√(v(x)^2 -1) •dx=∫1/x •dx
log(√(v(x)^2 -1) +v(x))=log(x)+c, где с - произвольная константа
Находим для:
v(x)=(e^-с +e^c •x^2)/2x
Упрощаем произвольные константы:
v(x)=1/2cx +cx/2
Вернемся к y(x)=xv(x) для подстановки:
y(x)=x(1/2cx +cx/2)
Упрощаем произвольные константы и получаем ответ:
y(x)=1/4c +cx^2
-
Автор:
esteban897 - 6 лет назад
-
0
-
-
Добавить свой ответ
-
На території Західної України романтизм пов`язаний із діяльістю___________, членами якої були__________________________
-
Предмет:
Українська література -
Автор:
peanut - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Первая труба наполняет бассейн за 20 минут а вторая за 5 минуты Вопрос за сколько они наполнят бассейн и там нельзя так 20-5=15
-
Предмет:
Математика -
Автор:
luisvrbd - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Прямая касается двух окружностей с центрами в точках O и P в точках A и B соответственно. Через точку С, в которой эти окружности касаются друг друга, проведена их общая касательная, пересекающая прямую AB в точке M. Найти PM, если AB = 8, ∠COM = α
-
Предмет:
Геометрия -
Автор:
fostervkdp - 6 лет назад
-
Ответов:
6 -
Смотреть
-
-
Traduisez en employant les tours présentatifs
1. мы любим музыку.
2 Завтра мы уезжаем.
3. люблю путешествия .
4.Что это за книги? Те, что вы прочли на каникулах?
5. Я смотрю телевизионные передачи об искусстве.
NB:теле (радио) передачи (`émissions d'art, sur les arts).
-
Предмет:
Французский язык -
Автор:
clover - 6 лет назад
-
Ответов:
1 -
Смотреть
-
