-
помогите, пожалуйста.
во вложении.
спасибо!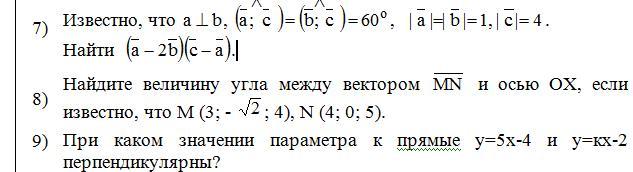
-
Предмет:
Математика -
Автор:
martínbyrd - 6 лет назад
-
Ответы 1
-
1. Рассмотрим треугольник ABC, в котором AB = AC = 4 (так как |c|=4), ∠ABC = 60°, ∠ACB = 60°. Тогда треугольник ABC - правильный, и каждая его сторона равна 4.
Пусть D - середина стороны BC, а E - точка на луче AB, такая что BE = |a| - b. Тогда треугольник AED - прямоугольный, и мы можем найти его высоту AD:
AD^2 = AE^2 - DE^2 = (|a| - b)^2 - (2^2) = |a|^2 - 2|a|b + 1 - 4 = |a|^2 - 2|a|b - 3.
Также заметим, что треугольник ACD - равнобедренный, поэтому AD = CD = 2.
Итак, мы знаем, что AD = 2, |c| = 4, и можем найти BD = CD - BD = 2 - √3.
Теперь рассмотрим выражение (а - 2Б)(с - а):
(а - 2Б)(с - а) = ас - а^2 - 2bс + 2ab = (ac - bc) - a^2 - 2bс + 2ab =
= c(|a| - b) - a^2 - 2bс + 2ab = 4|a| - 4 - a^2 - 2bс + 2ab.
Осталось заметить, что bс = |a|сos 60° = |a|/2 (так как с = 4), и подставить известные значения a и b:
4|a| - 4 - a^2 - |a| + 1 = 3|a| - a^2 - 3.
Ответ: 3|a| - a^2 - 3.
2. Вектор MN = N - M = (4-3; 0-(-2); 5-4) = (1; 2; 1).
Теперь найдем угол между вектором MN и осью OX:
cos α = (MN, OX) / |MN|*|OX| = (1*1 + 0*0 + 1*0) / √(1^2 + 2^2 + 1^2) * √(1^2 + 0^2 + 0^2) = 1 / √6.
Ответ: угол α между вектором MN и осью OX равен arccos(1/√6).
-
Автор:
Fedoseewa27 - 2 года назад
-
0
-
-
Добавить свой ответ
-
Решите пожалуйсто задачу => В тридев'ятому царстві є два сусідніх села, в яких: а) 101 ј 201 дворів b) 100і -201 дворів. Кожен місяць Соловій-розбійник і Змій Горинич по черзі спалюють декілька дворів в якому-небудь селі, причому число спалених дворів повинно ділитися на число дворіву другому селі. Програє той, кому нічого спалювати. Соловій-розбійник починає першим, чи зможе він спалити останній?
-
Предмет:
Математика -
Автор:
novak - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
2cos(П/2-x)=1 решить уравнение решение уравнение
-
Предмет:
Математика -
Автор:
lion4fxr - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Приведите из любых источников административного права по 5 примеров вертикальных, горизонтальных, диагональных, материальных, и процессуальных отношений.
-
Предмет:
Право -
Автор:
marliedudley - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он был вызван, – это …
А) Правило правой руки.
B) Правило левой руки.
C) Правило буравчика.
D) Правило Ленца.
E) Правило Герца.
