-
найти частное решение диф уравнения 2 порядка
номер 25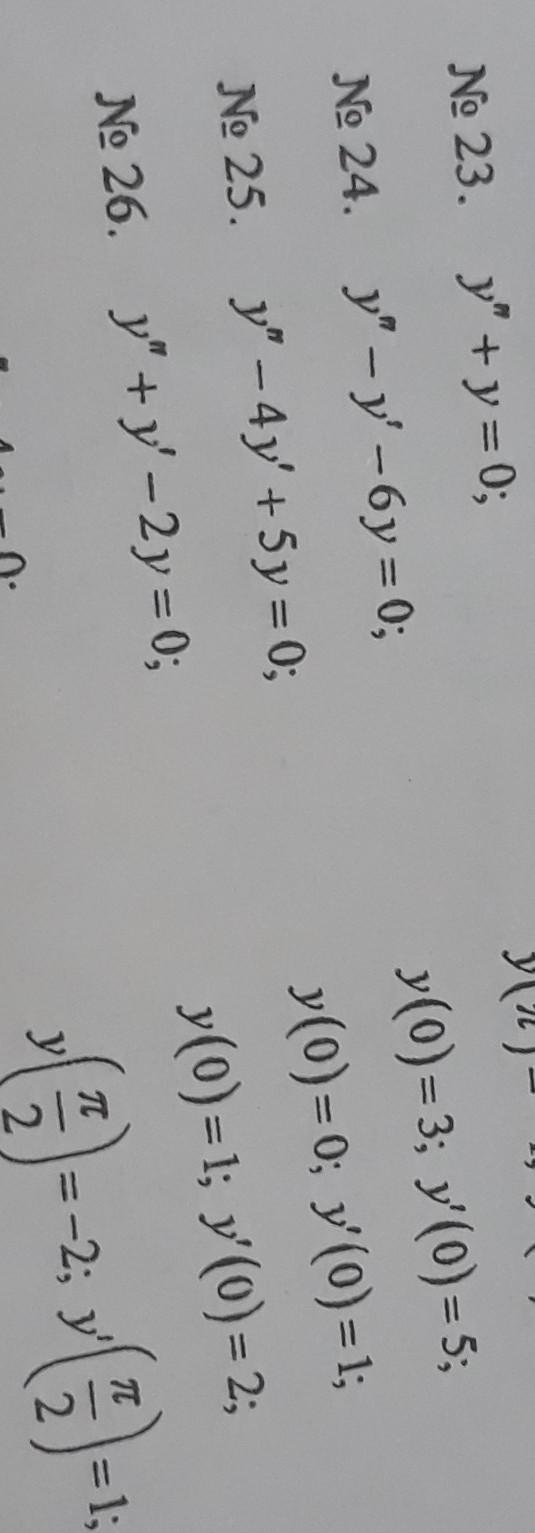
-
Предмет:
Математика -
Автор:
daphne31qb - 6 лет назад
-
Ответы 1
-
Ответ: y=e^(2*x)*sin(x).
Пошаговое объяснение:
Характеристическое уравнение k²-4*k+5=0 имеет комплексные корни x1=2+i и x2=2-i, поэтому общее решение имеет вид y=e^(2*x)*[C1*cos(x)+C2*sin(x)].
Производная y'=2*C1*e^(2*x)*cos(x)-C1*e^(2*x)*sin(x)+2*C2*e^(2*x)*sin(x)+C2*e^(2*x)*cos(x). Используя начальные условия, приходим к системе уравнений:
C1=0
2*C1+C2=1,
откуда C2=1. Значит, искомое частное решение таково: y=e^(2*x)*sin(x).
-
Автор:
mauricio721 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Здравствуйте помогите решить задачу по программированию на языке C++
Задача:Создать массив литературных произведений отсортировать в порядке увеличения количества символов в названии вывести на экран название с самым маленьким и самым большим количеством символов, с самым маленьким и самым большим количеством гласных, и самым маленьким и самым большим количеством согласных.-
Предмет:
Информатика -
Автор:
griffinlp20 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
На двух автоматах производятся одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата втрое больше производительности второго. Первый автомат производит в среднем 80% деталей первого сорта, а второй-90%. Взятая на удачу с конвейера деталь оказалась первого сорта. Найдите вероятность того, что эта деталь произведена первым автоматом
-
Предмет:
Математика -
Автор:
raquelramsey - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В параллелограме ABCD проведены биссектрисы углов A ,B ,C и D. Точка E является точкой пересечения биссектрис углов A и D , точка F является точкой пересечения биссектрис углов B и C . Докажите что отрезок EF параллелен AB и DC.
-
Предмет:
Геометрия -
Автор:
gregoriouvcu - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Как разделить 16 на 2/3 чтобы получилась число
-
Предмет:
Математика -
Автор:
mercedesmeyers - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
