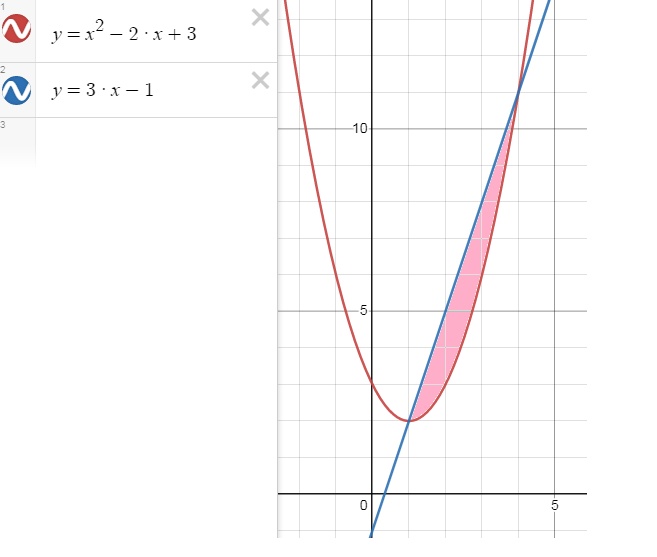
Найти площадь фигуры, ограниченной линиями: 𝑦 = 𝑥 2 − 2𝑥 + 3, 𝑦 = 3𝑥 − 1.

y1 = x^2 - 2x + 3; y2 = 3x - 1

Найти площадь фигуры, ограниченной линиями.

Решение:

Чтобы найти площадь фигуры, ограниченной линиями, нужно взять интеграл от этих функций.

Сначала находим пределы интегрирования - это точки пересечения линий.

Для этого приравняем функции друг к другу:

x^2 - 2x + 3 = 3x - 1

x^2 - 2x + 3 - 3x + 1 = 0

x^2 - 5x + 4 = 0

(x - 1)(x - 4) = 0

x1 = 1; x2 = 4

Возьмем какое-нибудь x Є (1; 4), например, x = 2, и посчитаем значения функций в этой точке:

y1(2) = 2^2 - 2*2 + 3 = 4 - 4 + 3 = 3

y2(2) = 3*2 - 1 = 6 - 1 = 5

y2(2) > y1(2)

Значит, на этом промежутке прямая y2(x) лежит выше параболы y1(x).

Значит, нужно из функции y2(x) вычесть функцию y1(x).

S = Integral(1; 4) (3x - 1 - x^2 + 2x - 3) dx = Integral(1; 4) (-x^2 + 5x - 4) dx =

= -x^3/3 + 5x^2/2 - 4x |(1; 4) = -4^3/3 + 5*4^2/2 - 4*4 - (-1^3/3 + 5*1^2/2 - 4*1) =

= -64/3 + 5*8 - 16 + 1/3 - 5/2 + 4 = -63/3 + 28 - 2,5 = -21 + 28 - 2,5 = 4,5

На картинке площадь закрашена.

Ответ: S = 4,5