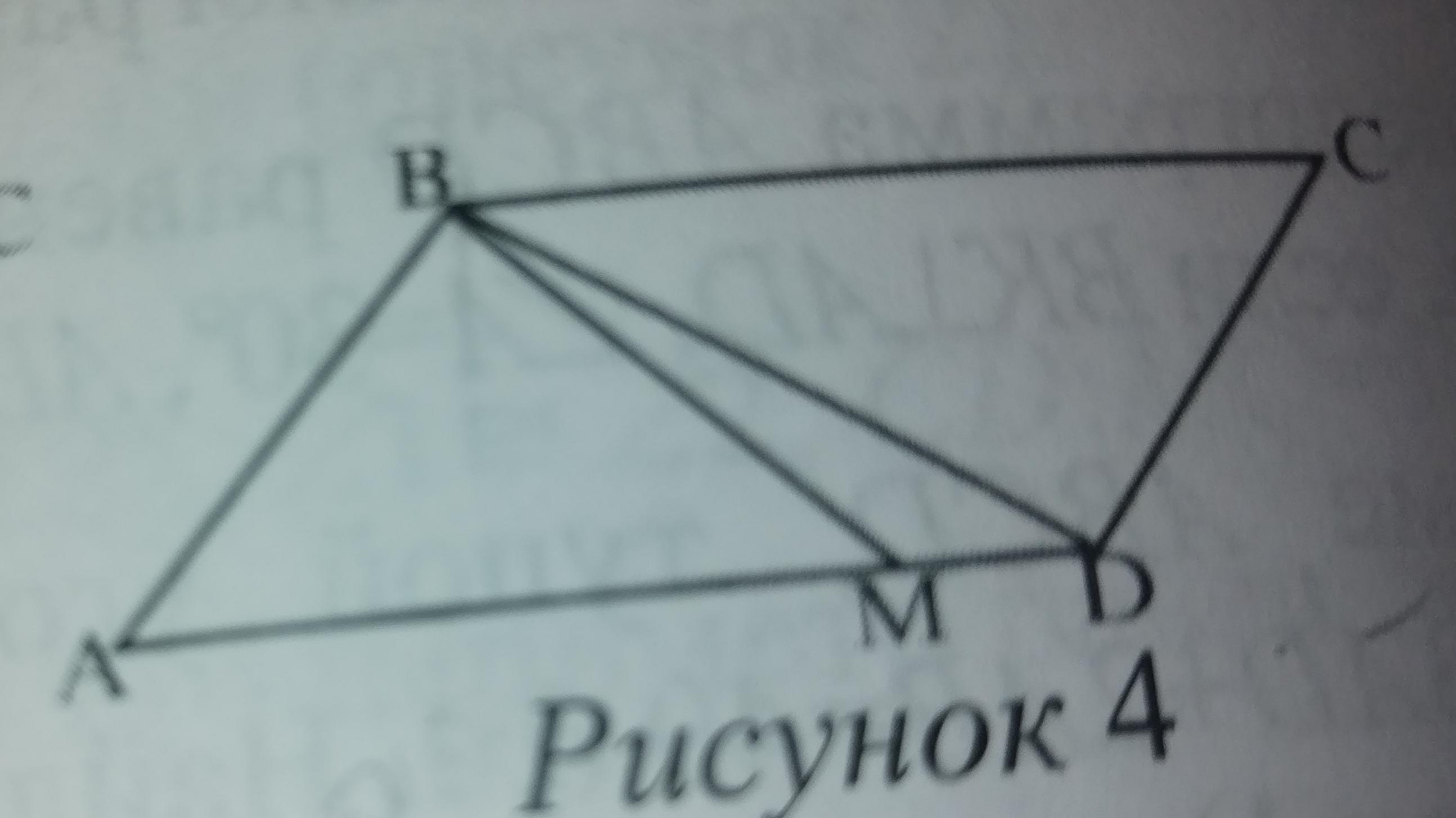
В параллелограмме ABCD, AM:MD=3:2. Найдите площадь треугольника ABM, если площадь параллелограмма равна 70 дм в кв. Даю 100 баллов

Ответ:

Давайте назовем длину AB "x".

Поскольку AM:MD = 3:2, мы можем написать:

AM = 3/5 * MD

И поскольку MD = x, мы имеем:

AM = 3/5 * x

Поскольку хэш-область параллелограмм ABCD 70 дм^2, мы можем записать:

x * AM = 70

Итак, подставляя AM = 3/5 * x, мы имеем:

х * 3/5 * х = 70

Расширение и решение для x:

(3/5)х^2 = 70

х^2 = 70 * 5/3

х^2 = 70 * 5/3 = 700/3

x = sqrt(700/3) = sqrt(100 * 7/3) = sqrt(100) * sqrt(7/3)

Итак, длина Бис x = 10 * sqrt(7/3).

Наконец, площадь треугольника И равна:

(1/2) x AM = (1/2) * x * 3/5 * x = (3/10) x^2 = (3/10) * (10 * sqrt(7/3))^2 = (3/10) * 100 * 7/3 = (3/10) * 700/3 = 210/3 = 70.

Следовательно, площадь треугольника И составляет 70 дм^2.

Пошаговое объяснение: