У прямокутній трапеції менша основа дорівнює 21 см. Обчислити площу трапеції, якщо довжина кола, вписаного в неї, дорівнює 24 см

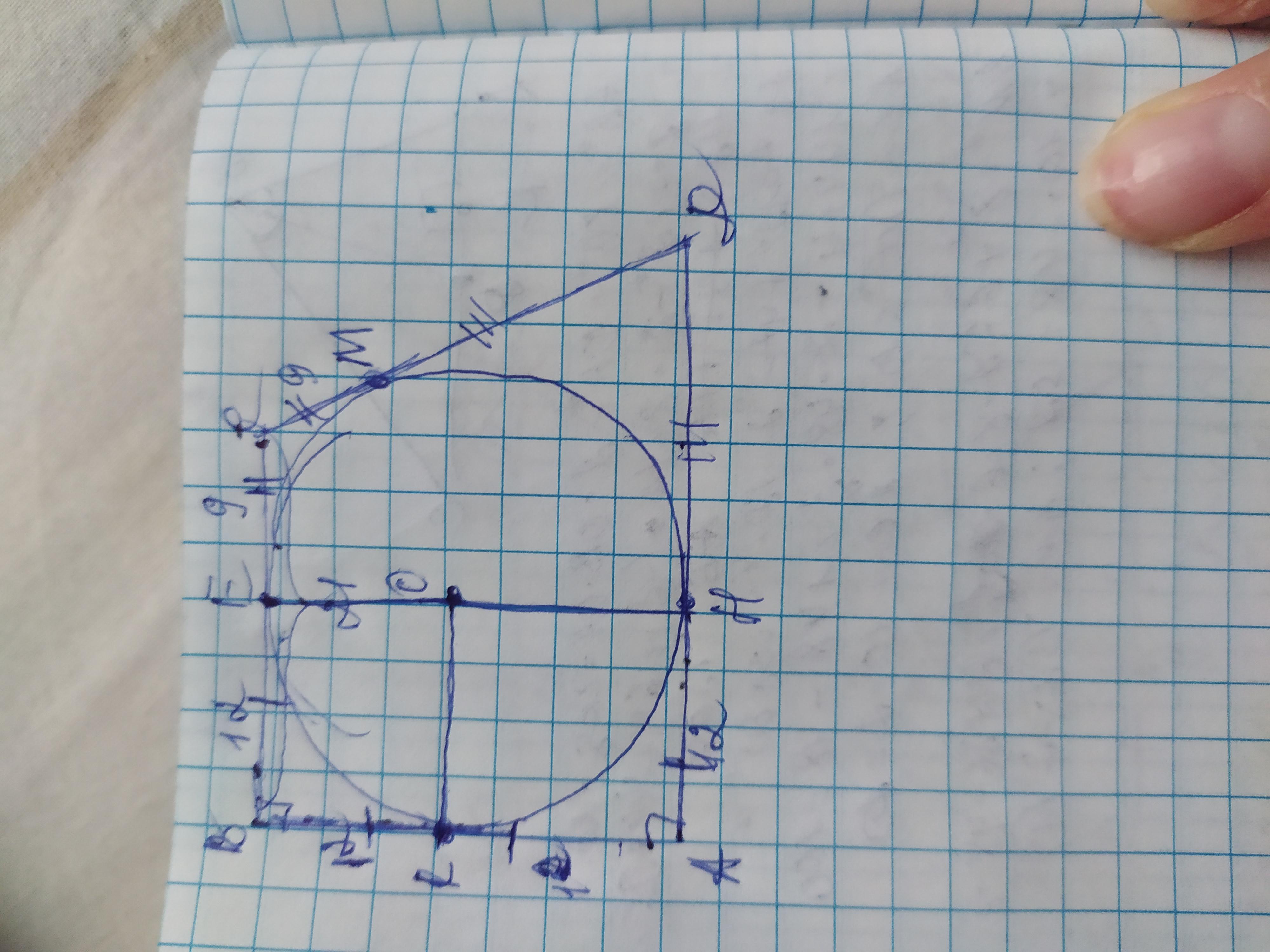
Відповідь: Объяснение: стороны трапеции являются касательными к вписанной окружности и отрезки касательных соединяясь в одной вершине равны от вершины до точки касания. Обозначим вершины трапеции А В С Д а точки касания К Е М Н, центр окружности О. Поэтому, ВК=ВЕ=АК=АН=радиусу, МД=НД, а ЕС=СМ. Так как нам известна длина окружности L, найдём её радиус, используя формулу длины окружности:

L=2πr

r=L/2π=24π/2π=12см.

Итак: r=12см

АВ и ЕН также являются высотами трапеции и равны диаметру:

АВ=ЕН= 12×2=24см

Если ВЕ=12см, то ЕС=21-12=9см

ЕС=СМ=9см

Теперь найдём основание АД, используя формулу нахождения радиуса:

r=√(CM×МД) поменяем местами левую и правую часть уравнения:

√(СМ×МД)=r

√(9×MД)=12. Возведём в квадрат левую и правую часть уравнения:

(√9×МД)²=12²

9МД=144

МД=144/9

МД=16см

МД=НД=16см

Тогда АД=АН+НД=12+16=28см

Теперь найдём площадь трапеции зная высоту и оба основания по формуле:

S=(ВС+АД)/2×АВ=

=(21+28)/2×24=49×12=588см²

Покрокове пояснення: