Помогите пожалуйста, очень срочно! равнобедренная трапеция имеет острые углы 60°, косую сторону и малое основание соответственно 40 см и 30 см. Определить площадь трапеции.

Для определения площади равнобедренной трапеции с острыми углами 60° и заданными сторонами, можно воспользоваться следующей формулой:

Площадь трапеции = (сумма оснований * высота) / 2

Высота трапеции можно найти, используя теорему Пифагора в одном из треугольников, образованных высотой, половиной большого основания и косой стороной трапеции:

высота^2 = косая сторона^2 - (половина большого основания)^2

Теперь подставим известные значения и решим:

Косая сторона = 40 см

Половина большого основания = 30 см / 2 = 15 см

высота^2 = 40^2 - 15^2 = 1600 - 225 = 1375

высота = √1375 ≈ 37.07 см

Теперь вычислим площадь:

Площадь = (30 см + 40 см) * 37.07 см / 2 ≈ 1853.5 кв.см

Итак, площадь равнобедренной трапеции составляет примерно 1853.5 квадратных сантиметра.

Ответ:

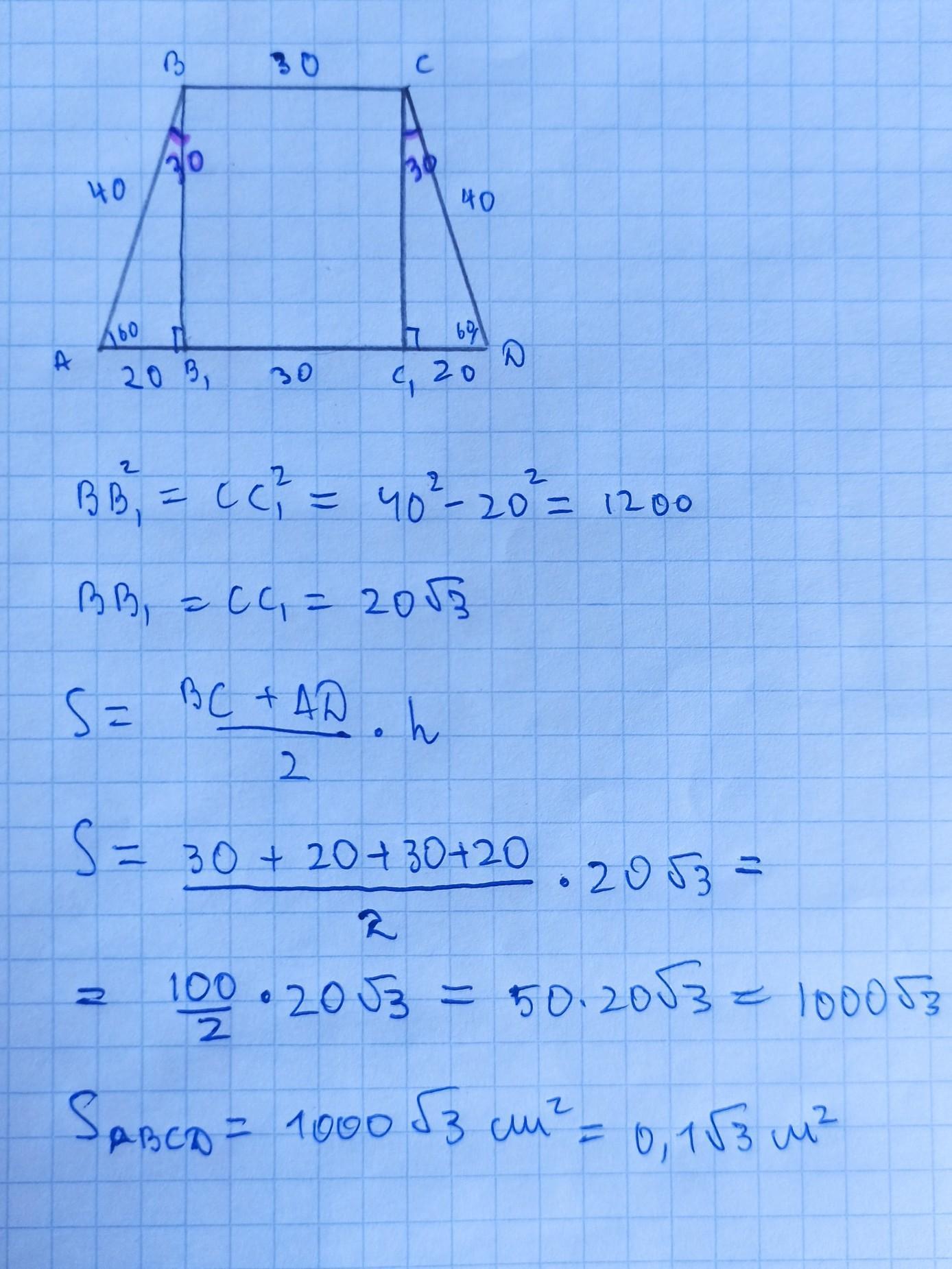
Решение на фото:

Пошаговое объяснение:

Если нужно, могу написать объяснение.