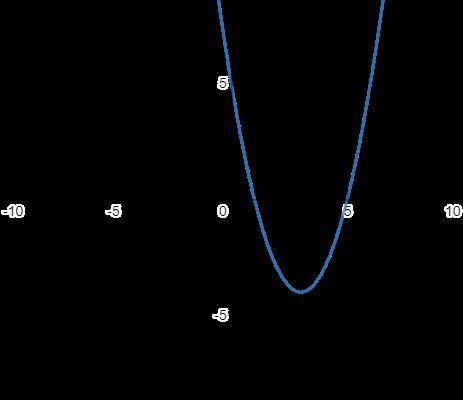
Постройте график функции y=x²-6x+5. Пользуясь графиком. найдите: 1) промежуток убывания функции; 2) множество решений неравенства x2-6x+5больше или равно 0.​

Ответ:

1) промежуток убывания: х∈(-∝;3)

2) x∈(-∝;1]∪[5;+∝)

Пошаговое объяснение:

графиком данной функции является парабола, ветви которой направлены вверх так как а>0.

Найдем точки пересечения параболы с осями координат:

если х=0, то у(0)=5 и график параболы пересекает ось ОУ в точке (0;5)

если у=0,  то x^{2} -6x+5=0= > (x-1)(x-5)=0 = > x_1=1 ,x_2=5

теперь осталось найти координаты вершины параболы: x_0=-\frac{b}{2a}=\frac{6}{2}=3 \\y_0(3)=9-18+5=-4

Следовательно х=3 ось симметрии параболы с вершиной (3;-4) и точками пересечения с осями ОХ: x_1=1\\x_2=5 и осью ОУ в точке (0;5)

зная все эти данные строим параболу.

1) промежуток убывания: х∈(-∝;3)

2) x∈(-∝;1]∪[5;+∝)