-
Решите пожалуйста пример по высшей математике
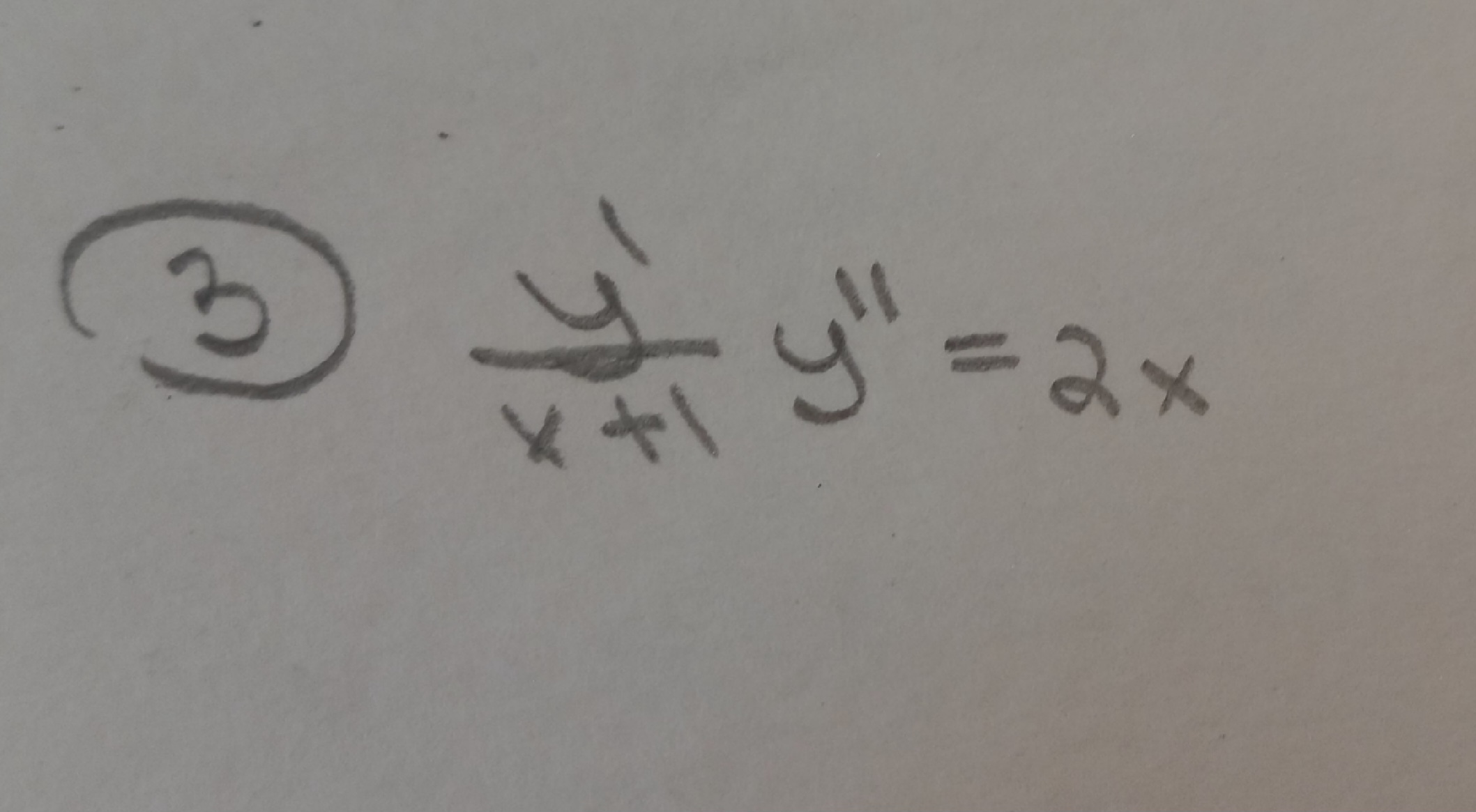
-
Предмет:
Математика -
Автор:
flurgadelsha - 2 года назад
-
Ответы 1
-
Данное дифференциальное уравнение является уравнением с разделяющимися переменными. Давайте найдем его решение.
Исходное уравнение: y'/x + 1 * y'' = 2x.
Умножим обе части уравнения на x, чтобы избавиться от дроби: y' + xy'' = 2x^2.
Перепишем уравнение в виде: xy'' + y' = 2x^2.
Далее, сделаем замену переменных: z = y'. Тогда y'' = z'.
Подставим замену в исходное уравнение: xz' + z = 2x^2.
Разделим обе части уравнения на x: z' + z/x = 2x.
Теперь это уравнение с разделяющимися переменными. Перенесем член z/x на другую сторону: z' = -z/x + 2x.
Разделим обе части уравнения на z - z'/z: z'/z = 2x - z/x.
Проинтегрируем обе части уравнения по переменной x: ln|z| = x^2 - ln|x| + C,
где C - произвольная постоянная.
Вернемся к исходной переменной y: z = y', поэтому ln|y'| = x^2 - ln|x| + C.
Возведем обе части уравнения в экспоненту: |y'| = e^(x^2 - ln|x| + C).
Упростим выражение в модуле: |y'| = e^(x^2 + C - ln|x|).
Поскольку C - произвольная константа, можем записать ее как C = ln|A|, где A - произвольная константа.
Тогда уравнение примет вид: |y'| = e^(x^2 + ln|A| - ln|x|).
Сократим логарифмы: |y'| = e^(ln|A| + x^2 - ln|x|).
Упростим выражение: |y'| = e^(ln|Ax^2 / |x||).
Уберем модуль из выражения: y' = Ax^2 / |x|.
Таким образом, получаем общее решение дифференциального уравнения: y(x) = ∫(Ax^2 / |x|)dx,
где A - произвольная постоянная.
-
Автор:
Fedoseewa27 - 2 года назад
-
-1
-
-
Добавить свой ответ
-
ДАЮ 50 БАЛЛОВ. СРОЧНО.
У воду об’ємом 7 л , взяту при температурі 9 °С, поклали шматок заліза,
нагрітий до 450 °С. Визначте масу заліза, якщо температура суміші стала
дорівнювати 40 °С. Питома теплоємність заліза дорівнює 500 Дж
кг·°С
. Питома теплоємність води 4200 Дж
/кг·°С
, густина води 1000 кг/м3
.
-
Предмет:
Физика -
Автор:
robertoobrien - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Gramma Task 3. Complete the sentence. Use the verbs in brackets and write true sentences in Present Simple (to play) computer games. (not to work) very hard. 1. Anna 2. You 3. 4. I 5. My sister (to go) (do/does) you have a breakfast in the morning? (to like) apples. to bed at nine.(пожалуйста даю 50баллов)
-
Предмет:
Английский язык -
Автор:
joebrady - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Решите пожалуйста пример по высшей математике
-
Предмет:
Математика -
Автор:
flurgadelsha - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Решите пожалуйста пример по высшей математике
-
Предмет:
Математика -
Автор:
flurgadelsha - 2 года назад
-
Ответов:
1 -
Смотреть
-
