-
Решите пожалуйста пример по высшей математике
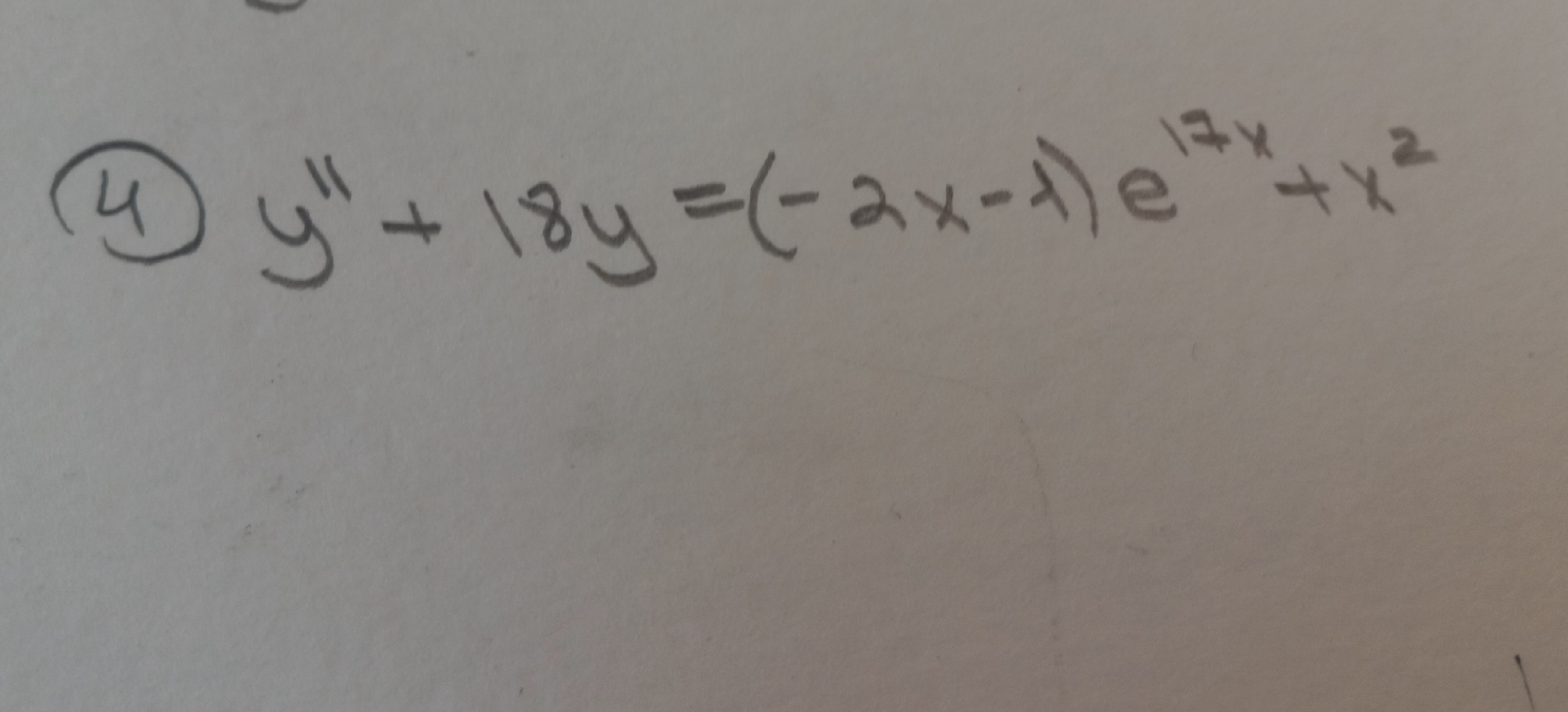
-
Предмет:
Математика -
Автор:
flurgadelsha - 2 года назад
-
Ответы 1
-
Данное уравнение является линейным неоднородным дифференциальным уравнением второго порядка. Для его решения, требуется применить метод вариации постоянных.
1. Найдем общее решение соответствующего однородного уравнения y" + 18y = 0. Его характеристическое уравнение будет иметь вид r^2 + 18 = 0. Решив это уравнение, получим два комплексных корня: r1 = 3i и r2 = -3i. Тогда общее решение однородного уравнения будет иметь вид yh = c1cos(3x) + c2sin(3x), где c1 и c2 - произвольные постоянные.
2. Найдем частное решение неоднородного уравнения с помощью метода вариации постоянных. Предположим, что частное решение имеет вид yp = v(x)cos(3x) + w(x)sin(3x). Тогда вычислим производные первого и второго порядка этой функции:
yp' = v'(x)cos(3x) + v(x)-3sin(3x) + w'(x)sin(3x) + w(x)3cos(3x),
yp" = v"(x)cos(3x) + v'(x)-3sin(3x) + v'(x)[-3sin(3x)] + v(x)-9cos(3x) + w"(x)sin(3x) + w'(x)3cos(3x) + w'(x)[3cos(3x)] + w(x)-9sin(3x).
Подставим yp и его производные в исходное уравнение и приравняем коэффициенты при одинаковых тригонометрических функциях:
v"(x)cos(3x) + v'(x)-3sin(3x) + v'(x)[-3sin(3x)] + v(x)-9cos(3x) + w"(x)sin(3x) + w'(x)3cos(3x) + w'(x)[3cos(3x)] + w(x)-9sin(3x) + 18[v(x)cos(3x) + w(x)sin(3x)] = (-2x-1)e^(17x) + x^2.
Собирая коэффициенты при одинаковых функциях, получим систему уравнений:
v"(x) - 9v(x) + 18v(x) = (-2x-1)e^(17x) + x^2,
w"(x) - 9w(x) + 18w(x) = 0.
Упростим эти уравнения:
v"(x) + 9v(x) = (-2x-1)e^(17x) + x^2,
w"(x) + 9w(x) = 0.
Решим первое уравнение методом вариации постоянных, применяя формулу Лагранжа:
v(x) = c1(x)cos(3x) + c2(x)sin(3x).
Найдем производные вариаций:
v'(x) = c1'(x)cos(3x) - 3c1(x)sin(3x) + c2'(x)sin(3x) + 3c2(x)cos(3x),
v"(x) = c1"(x)cos(3x) - 6c1'(x)sin(3x) - 9c1(x)cos(3x) + c2"(x)sin(3x) + 6c2'(x)cos(3x) - 9c2(x)sin(3x).
Подставим v(x), v'(x) и v"(x) в первое уравнение системы и приравняем коэффициенты при одинаковых тригонометрических функциях:
c1"(x)cos(3x) - 6c1'(x)sin(3x) - 9c1(x)cos(3x) + c2"(x)sin(3x) + 6c2'(x)cos(3x) - 9c2(x)sin(3x) + 9[c1(x)cos(3x) + c2(x)sin(3x)] = (-2x-1)e^(17x) + x^2.
Собирая коэффициенты при одинаковых тригонометрических функциях, получим систему уравнений вариаций:
c1"(x) - 9c1(x) + 9c1(x) = (-2x-1)e^(17x) + x^2,
c2"(x) - 9c2(x) + 9c2(x) = 0.
Упростим эту систему:
c1"(x) = (-2x-1)e^(17x) + x^2,
c2"(x) = 0.
Интегрируя эти уравнения, найдем вариации:
c1(x) = (-1/34)e^(17x) - (1/6)x^2 + c3,
c2(x) = c4.
Теперь, подставим вариации в общее решение частного решения неоднородного уравнения:
yp = v(x)cos(3x) + w(x)sin(3x) = c1(x)*cos(3x) + c2(x)*sin(3x)cos(3x) + [c3cos(3x) + c4sin(3x)]sin(3x),
где c1(x) = (-1/34)e^(17x) - (1/6)x^2 + c3 и c2(x) = c4.
Таким образом, получаем частное решение неоднородного уравнения y" + 18y = (-2x-1) e^(17x) + x^2:
yp = (-1/34)e^(17x) - (1/6)x^2 + c3cos(3x) + [c3cos(3x) + c4sin(3x)]sin(3x) + c1cos(3x) + c2sin(3x),
где c1 и c2 - произвольные постоянные, а c3 и c4 - произвольные функции.
-
Автор:
Fedoseewa27 - 2 года назад
-
1
-
-
Добавить свой ответ
-
Gramma Task 3. Complete the sentence. Use the verbs in brackets and write true sentences in Present Simple (to play) computer games. (not to work) very hard. 1. Anna 2. You 3. 4. I 5. My sister (to go) (do/does) you have a breakfast in the morning? (to like) apples. to bed at nine.(пожалуйста даю 50баллов)
-
Предмет:
Английский язык -
Автор:
joebrady - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Решите пожалуйста пример по высшей математике
-
Предмет:
Математика -
Автор:
flurgadelsha - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Решите пожалуйста пример по высшей математике
-
Предмет:
Математика -
Автор:
flurgadelsha - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Поверхневий апарат клiтни складаєься з
наступних систем
варіанти відповідей:
а)плазматичної мембрани
в)цитоплазми
б)клітинного центру
г)надмембранного і
пiдмембранного комплексів
д)ядра
-
Предмет:
Биология -
Автор:
mini skirt - 2 года назад
-
Ответов:
1 -
Смотреть
-
