-
найти частное решение дифференциального уравнения, удовлетворяющее начальное условие
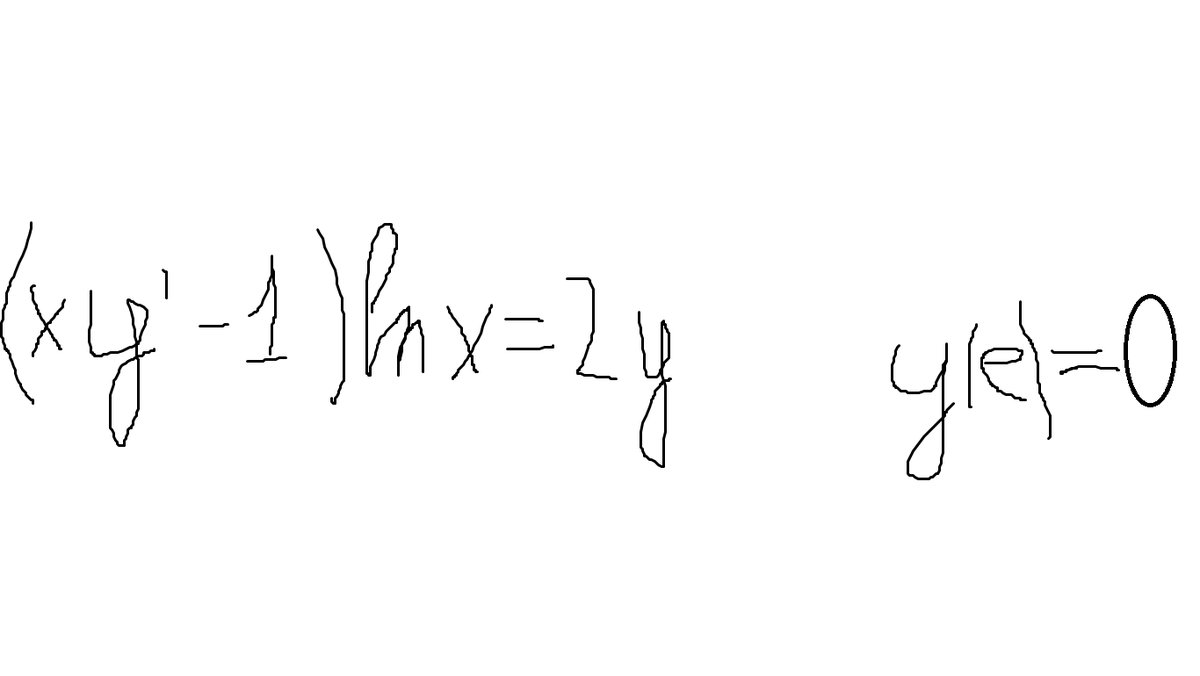
-
Предмет:
Математика -
Автор:
gizmobanq - 6 лет назад
-
Ответы 1
-
Решить дифференциальное уравнение (xy' - 1)ln(x) = 2y xy' -1 = 2y/ln(x) y' - 2y/(xln(x)) - 1/x = 0 Получили линейное дифференциальное уравнение Решим методом Лагранжа Решаем вначале уравнение y' - 2y/(xln(x)) = 0 y' = 2y/(xln(x)) y'/y = 2/(xln(x)) dy/y = 2dx/(xln(x)) ln(y) = 2ln(ln(x)) + ln(C²) y = Cln²(x) Заменяем C на C(x) то есть решение дифференциального уравнения y' - 2y/(xln(x)) - 1/x = 0 ищем в виде y = C(x)ln²(x) y' = С'(x)ln²(x) + 2C(x)ln(x)/x Подставляем в дифференциальное уравнение С'(x)ln²(x) + 2C(x)ln(x)/x - 2С(x)ln²(x)/(xln(x)) - 1/x = 0 С'(x)ln²(x) + 2C(x)ln(x)/x - 2С(x)ln(x)/x - 1/x = 0 С'(x)ln²(x) - 1/x = 0 С'(x)ln²(x) = 1/x С'(x) = 1/(xln²(x)) dC(x) = dx/(xln^2(x)) Интегрируем обе части уравнения С(x) = -1/ln(x) + C Запишем общее решение дифференциального уравнения y = (-1/ln(x) + C)ln²(x) = -ln(x) + Cln²(x) Найдем частное решение при y(e)=0 y(e)=-ln(e) + Cln²(e) = -1 +C*1² = C - 1 C - 1 = 0 C = 1 Запишем частное решение дифференциального уравнения y = ln²(x) - ln(x) Ответ: y = ln²(x) - ln(x)
-
Автор:
benítez72 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
основные ценности каждой религии?
-
Предмет:
Обществознание -
Автор:
kaiden0ddl - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
сочинение по теме спорт на английском с переводом. Срочно! !!
-
Предмет:
Английский язык -
Автор:
margaritachambers - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Осуществить химические превращения
P-P2O5-H3PO4-Na3PO4-NaCL
-
Предмет:
Химия -
Автор:
coralieve2m - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Синонім до вислова ловиш Ґави
-
Предмет:
Українська література -
Автор:
hartman - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
