-
ЗДРАВСТВУЙТЕ! ПОМОГИТЕ РЕШИТЬ ПРИМЕР ПОДРОБНО С РЕШЕНИЕМ. ЗАРАНЕЕ СПАСИБО.
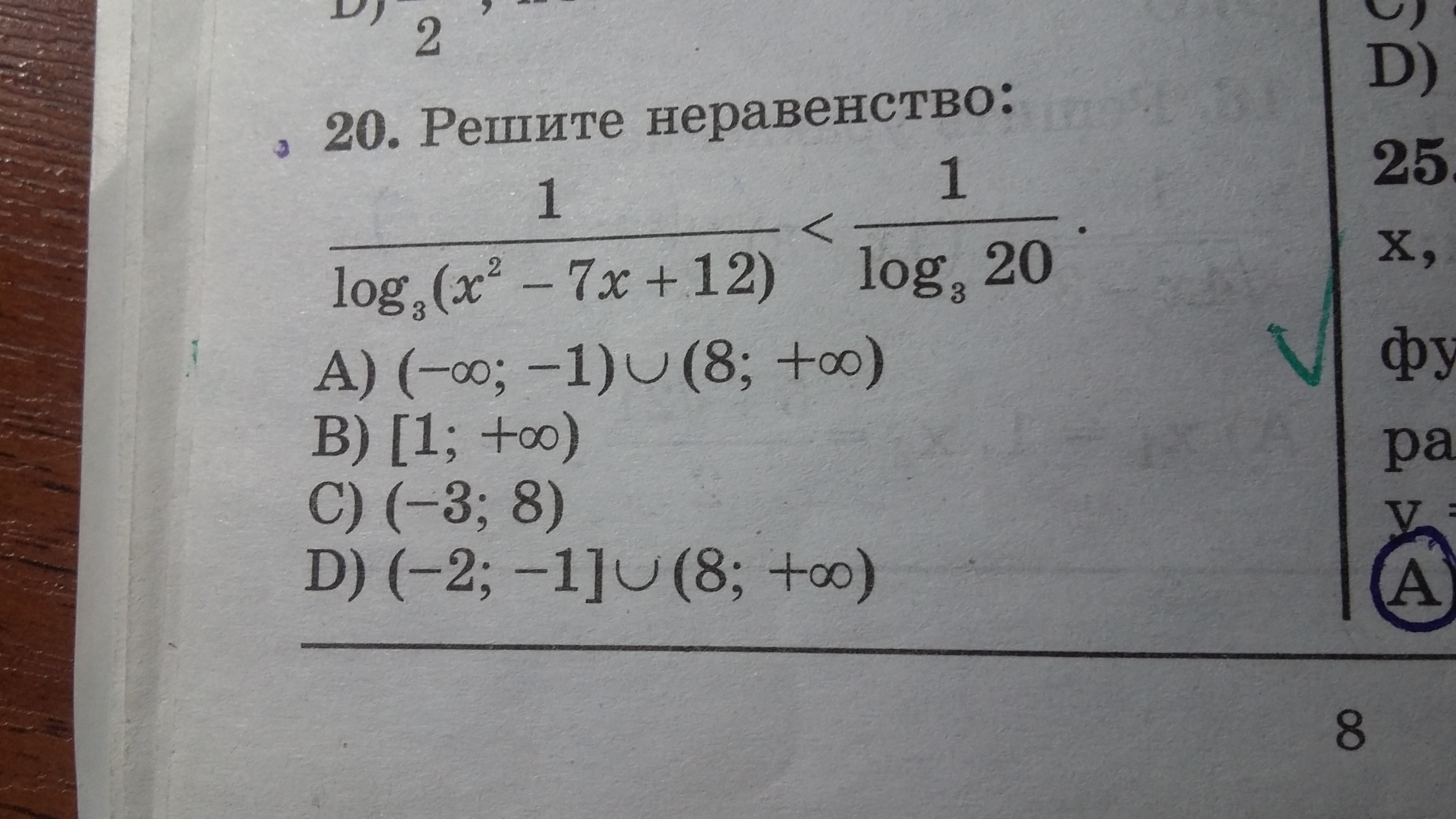
-
Предмет:
Алгебра -
Автор:
nehemiah8xfu - 6 лет назад
-
Ответы 5
-
мне не очень понятен один момент. Как вы пришли к такому виду log(3) x^2-7x+12
-
Автор:
luis2ypo - 6 лет назад
-
0
-
-
то есть log(3) x^2-7x+12 < log(3) 20
-
Автор:
oliverbnag - 6 лет назад
-
0
-
-
К сожалению, думаю, ваш ответ неверен, хоть и совпадает с одним из предложенных. Но там нет верного ответа! Попробуйте подставить, например, 2,5. Оно удовлетворяет неравенству, хотя и не входит в указанные вами промежутки
-
Автор:
calvingreene - 6 лет назад
-
0
-
-
Ответ:.........:...........

-
Автор:
lolafoley - 6 лет назад
-
0
-
-
Поскольку log3 20 > 0, возможны два случая:
log3 (x^2 - 7x + 12) < 0
log3 (x^2 - 7x + 12) > log3 20.
Первый случай:
log3 (x^2 - 7x + 12) < 0
0 < x^2 - 7x + 12 < 1
x^2 - 7x + 12 > 0
x^2 - 7x + 12 = 0
По теореме Виета:
x = 3
x = 4
x є (-оо; 3) U (4; +oo)
x^2 - 7x + 12 < 1
x^2 - 7x + 11 < 0
x^2 - 7x + 11 = 0
D = 49 - 44 = 5
x = 7-sqrt5 / 2
x = 7+sqrt5 / 2
x є (7-sqrt5 / 2; 7+sqrt5 / 2)
Решением первого случая есть пересечение (-оо; 3) U (4; +oo) и (7-sqrt5 / 2; 7+sqrt5 / 2). Поэтому x є (7-sqrt5 / 2; 3) U (4; 7+sqrt5 / 2).
Второй случай:
log3 (x^2 - 7x + 12) > log3 20
x^2 - 7x + 12 > 20
x^2 - 7x - 8 > 0
x^2 - 7x - 8 = 0
По теореме Виета:
x = -1
x = 8
x є (-оо; -1) U (8; +oo)
Общим решением неравенства есть объединение решений двух рассмотренных случаев:
x є (-оо; -1) U (7-sqrt5 / 2; 3) U (4; 7+sqrt5 / 2) U (8; +oo).

-
Автор:
greyson - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Совместным решением двух уравнений найдём точку пересечения прямых 3x+4y-9=0 и 2x+3y-7=0
-
Предмет:
Математика -
Автор:
lucianon1mj - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Ионное строение имеет:
1) вода
2) сероводород
3) азот
4) сульфид калия - Два поезда вышли одновременно навстречу друг другу из пунктов А и Б. После прибытия соответственно в пункты А и Б они сразуже развурнулись и начили движение в обратном направлении.1 раз они встретились за 120 км от пункта Б,а 2-за 60 км от А чрез 6 часов после 1 встречи. Найдите растояния между пунктами А и Б.Зарание спасибо!!
-
Задание 1.
Предложен перечень веществ: H2O, CaO, NaOH, SO3, H2SO4, CuSO4, Cu, С, KCl, P2O5. Выпишите из него формулы веществ: а) с ионной связью; б) с ковалентной связью.
