Ответы 1
-
Ответ:
Применяем свойствa степеней :
\bf \Big(\dfrac{a}{b}\Big)^{k}=\dfrac{a^{k}}{b^{k}}\ ,\ \ \Big(-1\Big)^{2n-1}=-1\ ,\ \Big(-1\Big)^{2n}=1 .
Смешанные числа сначала переводим в неправильные дроби .
\bf \displaystyle \Big(\frac{3}{4}\Big)^2\cdot 1\frac{1}{3}=\Big(\frac{3}{4}\Big)^2\cdot \frac{4}{3}=\frac{3}{4}\ \ ,\ \ \ \ 3^4\cdot \Big(-\frac{2}{3}\Big)^3=-3^4\cdot \frac{2^3}{3^3}=-3\cdot 8=-24\\\\\\1:\Big(-\frac{1}{3}\Big)^3=-1\cdot 3^3=-27\ \ \ ,\ \ \ \ \ \Big(\frac{3}{5}\Big)^2=\frac{3^2}{5^2}=\frac{9}{25}\\\\\\\frac{0,2^4}{40}=\frac{\Big(\dfrac{1}{5}\Big)^4}{40}=\frac{1}{5^4\cdot 40}=\frac{1}{625\cdot 40}=\frac{1}{25000}\ ,
\bf \displaystyle \frac{1,8}{0,3^2}=\frac{1,8}{\dfrac{3^2}{10^2}}=\frac{1,8\cdot 100}{9}=\frac{180}{9}=20\ \ ,\\\\\\\frac{1}{(-0,1)^3}=\frac{1}{\Big(-\dfrac{1}{10}\Big)^3}=-10^3=-1000\\\\\\\frac{1,6}{(0,4)^2}=\frac{1,6}{0,4\ \cdot \ 0,4}=\frac{16}{4\cdot \ 0,4}=\frac{4}{0,4}=\frac{40}{4}=10\\\\\\\Big(2\frac{1}{5}\Big)^2=\Big(\frac{11}{5}\Big)^2=\frac{11^2}{5^2}=\frac{121}{625}\ \ ,\\\\\\\Big(-3\frac{1}{3}\Big)^3=\Big(-\frac{10}{3}\Big)^3=-\frac{10^3}{3^3}=-\frac{1000}{27}=-37\frac{1}{27}
\bf \displaystyle \Big(-1\frac{2}{3}\Big)^4=\Big(-\frac{5}{3}\Big)^4=\frac{5^4}{3^4}=\frac{625}{81}=7\frac{58}{81}\\\\\\\Big(5\frac{1}{4}\Big)^2=\Big(\frac{21}{4}\Big)^2=\frac{21^2}{4^2}=\frac{441}{16}=27\frac{9}{16}


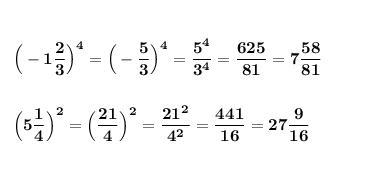
-
Автор:
kaleb224 - 2 года назад
-
5
-
-
Добавить свой ответ
- 23. Розв'яжiть задачу складанням системи лiнiйних рівнянь із 2 змінними. З двох селищ одночасно вирушили назустріч один одному два пішоходи і зустрілись через 3 год. Вiдстань між селищами 30км. Один з пішоходів пройшов до зустрiчi на 6 км більше, ніж другий. Знайдіть швидкiсть кожного пішохода.
- площадь трапеции ABCD равна 24. основания ДС и АВ равны соответственно 6 и 2. Точка Е лежит на стороне ВС так, что ВЕ=2ЕС. Найдите площадь треугольника АДЕ??
-
1 VOCABULARY colours, adjectives, modifiers Put the letters in the correct order to make colours. a 1 ehiwt 2 iknp 3 rde 4 rgaone 5 ewlyol 6 nerge 7 ebul 8 bonwr 9 ryeg 10 Ikabc white
-
Предмет:
Английский язык -
Автор:
schmidt - 2 года назад
-
Ответов:
1 -
Смотреть
-
- один із кутів паралелограма дорівнює півсумі трьох інших його кутів.знайдіть величину меншого кута
