-
Очень нужно решение... не пугайтесь что 3 в 1... оооч буду благодарен.
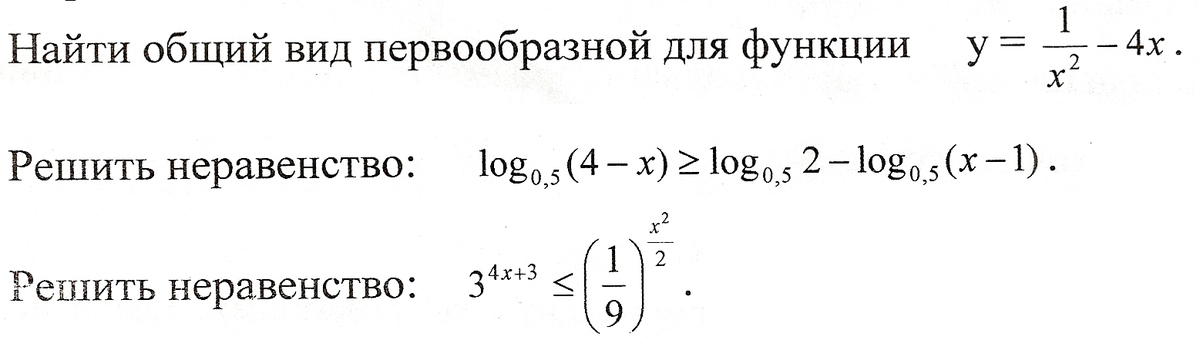
Ответы 1
-
1) у = 1/х² - 4х
F(x) = ∫(1/х² - 4х)dx + C
F(x) = -1/х - 4х²/2 + C
F(x) = -1/х - 2х² + C
2) log₀₅(4 - x) ≥ log₀₅ 2 - log₀₅(x - 1)
ОДЗ: 4 - х > 0 ⇒ х < 4
х - 1 > 0 ⇒ х > 1
х∈(1; 4)
log₀₅(4 - x) ≥ log₀₅ (2/(x - 1))
Поскольку основание логарифма 0,5< 1, то числа связывает отношение неравенства, обратное тому, что связывает логарифмы:
4 - x ≤ 2/(x - 1)
(4 - x)·(x - 1) ≤ 2
4х - х² - 4 + х - 2 ≤ 0
- х²+ 5х - 6 ≤ 0
найдём нули функции у = - х²+ 5х - 6
- х²+ 5х - 6 = 0
D = 25 + 24 = 1
x₁ = (-5 - 1):(-2) = 3
x₂ = (-5 + 1):(-2) = 2
Поскольку график функции у = - х²+ 5х - 6 - квадратная парабола веточками вниз, то неравенство - х²+ 5х - 6 ≤ 0 справедливо при х∈(-∞; 2] и [3; +∞)
Сопоставим это решение с ОДЗ: х∈(1; 4) и сделаем вывод, что
исходное неравенство log₀₅(4 - x) ≥ log₀₅ 2 - log₀₅(x - 1) справедливо при
х∈(1; 2] и [3; 4)
3)3^(4х + 3) ≤ (1/9)^0.5x²
3^(4х + 3) ≤ 3^(-x²)
Поскольку основание степени 3>1, то между показателями степени имеет место то же самое соотношение, что и между числами:
4х + 3 ≤ -x²
x² + 4х + 3 ≤ 0
найдём нули функции у = x² + 4х + 3
x² + 4х + 3 = 0
D = 16 - 12 = 4
√D = 2
x₁ = (-4 - 2):2 = -3
x₂ = (-4 + 2):2 = -1
Поскольку график функции у = x² + 4х + 3 - квадратная парабола веточками вверх, то неравенство x² + 4х + 3 ≤ 0 справедливо при х∈ [-3;-1]
Ответ: х∈ [-3;-1]
-
Автор:
jase7gfp - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Sin((Pi/4)+α)=(√2/2)*( Sinα+Cosα)
-
пусть n натуральное число. какая цифра стоит сразу после запятой в десятичной записи числа sqrt(n^2+n) ? я знаю что 4 докажите.
-
Предмет:
Математика -
Автор:
destineectr5 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите,пожалуйста,написать условия задачи. Мама разложила 15 вишенок на 3 торта,поровну на каждый торт.Сколько вишенок на каждом торте?
-
Предмет:
Математика -
Автор:
abelwilliams - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
y=x в квадрате+6x - 15 исследовать на exdr минимум
-
Предмет:
Математика -
Автор:
messiahmlfu - 6 лет назад
-
Ответов:
2 -
Смотреть
-
