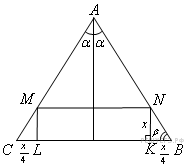
Основание равнобедренного треугольника равно 40, косинус угла при вершине равен 15/17. Две вершины прямоугольника лежат на основании треугольника, а две другие — на боковых сторонах. Найдите площадь прямоугольника, если известно, что одна из его сторон вдвое больше другой.

cosA=15/17⇒sinA=√1-225/289=√64/289=8/17⇒tgA=8/15tgA=2tg(A/2)/(1-tg²(A/2))=8/1530tg(A/2)=8-8tg²(A/2)tg(A/2)=m4m²+15m-4=0D=225+64=289m1=(-15-17)/8=-4 не удов услm2=(-15+17)/8=1/4⇒tg(A/2)=1/4tg(A/2)=CL/MLML=x, CL=20-x(20-x)/x=1/480-4x=x5x=80x=16-MLLK=2ML=32S=32*16=512