-
В равнобедренном треугольнике DBT проведена биссектриса TM угла T у основания DT,
∡TMB=72°. Определи величины углов данного треугольника (если это необходимо, округли ответ до тысячных).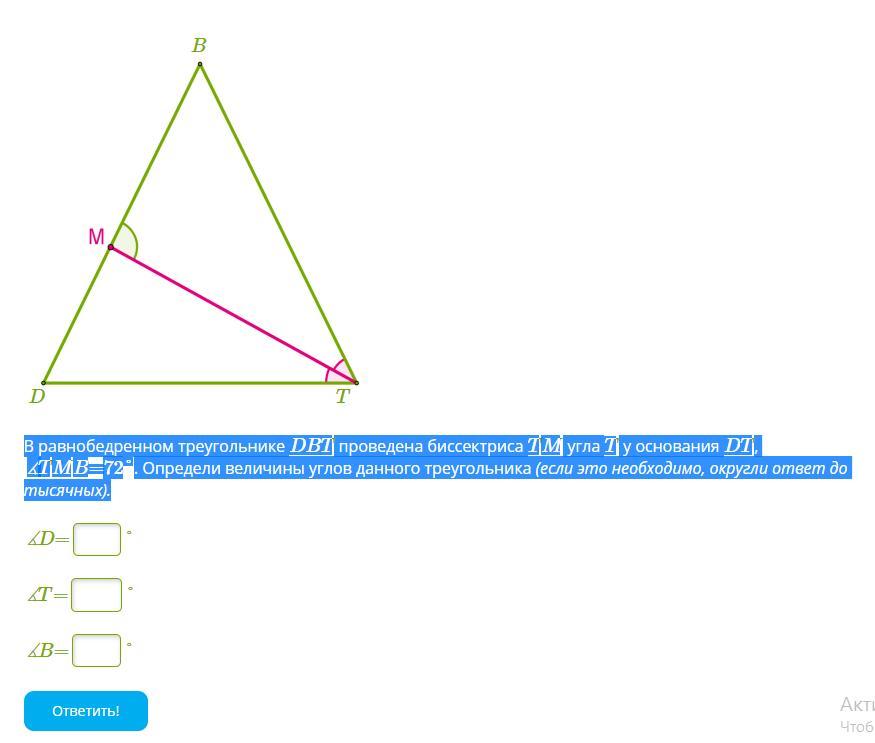
Ответы 1
-
В равнобедренном треугольнике DBT биссектриса TM делит угол T пополам, поэтому ∡DTM = ∡MTB.
Известно, что ∡TMB = 72°.
Так как сумма углов треугольника равна 180°, то ∡DTM + ∡MTB + ∡TMB = 180°.
Подставим известные значения:
∡DTM + ∡MTB + 72° = 180°.
Также, так как DBT - равнобедренный треугольник, то ∡DTM = ∡MTD.
Заменим ∡DTM на ∡MTD:
∡MTD + ∡MTB + 72° = 180°.
Теперь заменим ∡MTB на ∡DTM:
∡MTD + ∡DTM + 72° = 180°.
Так как ∡MTD = ∡DTM, заменим ∡MTD на ∡DTM:
∡DTM + ∡DTM + 72° = 180°.
Упростим уравнение:
2∡DTM + 72° = 180°.
Вычтем 72° из обеих сторон:
2∡DTM = 108°.
Разделим на 2:
∡DTM = 54°.
Таким образом, ∡DTM = ∡MTB = 54°, а ∡TMB = 72°.
В равнобедренном треугольнике DBT углы имеют следующие величины:
∡DTM = ∡MTB = 54°
∡TMB = 72°
-
Автор:
Fedoseewa27 - 2 года назад
-
0
-
-
Добавить свой ответ
-
угол С-90 гр
Найти Уголы А и В
Пожалуйста -
Помогите пожалуйста нужно написать сочинение на тему"моё любимое место"
-
Предмет:
Английский язык -
Автор:
conor35 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Дано: угол ADC=90
угол DAC=40
CAB=50
Доказать: BC II AD-
Предмет:
Геометрия -
Автор:
abramclayton - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Найдите длины катетов прямоугольного треугольника, один из углов которого равен 30° , если один из катетов на 30 см короче гипотенузы.
