Помогите!!!! Внутри рисунок!!!!

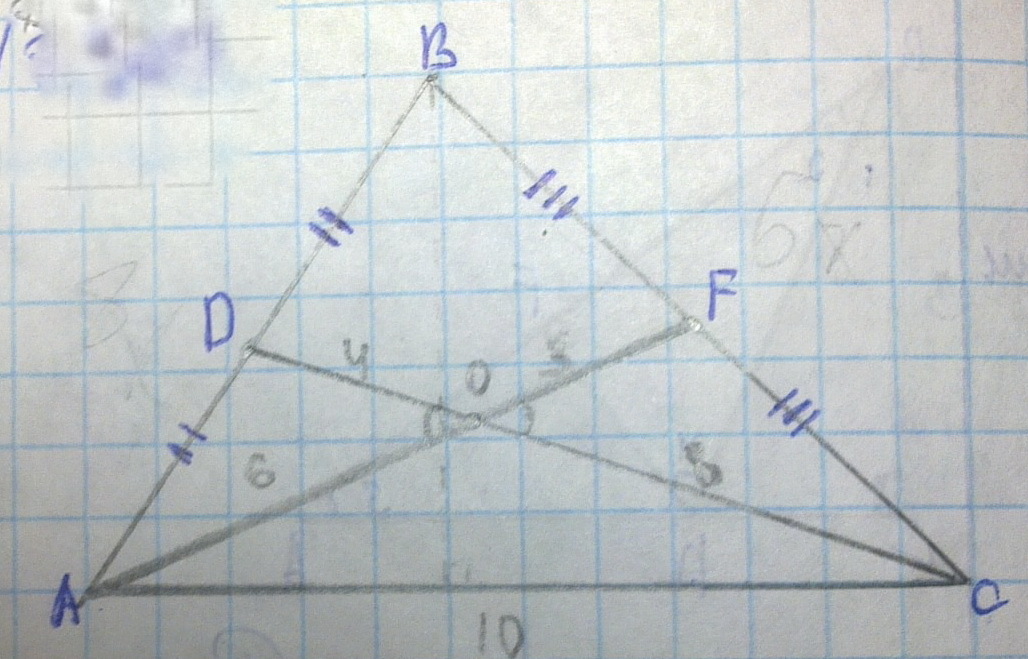
Одна из сторон треугольника равна 10, а медианы, проведенные к двум другим сторонам, равны 9 и 12. Найдите площадь треугольника.

 

Отрезки медиан от вершин до точки их пересечения равны 2/3 их длины, то есть 6 и 8. Поэтому треугольник АОС имеет стороны 6,8,10, то есть это "египетский" треугольник (6^2 + 8^2 = 10^2). То есть угол АОС прямой. Площадь АОС равна 6*8/2 = 24. А площадь всего треугольника АВС равна утроенной площади АОС, то есть 72.

Напоминаю - три медианы делят любой трегольник на 6 треугольников, равных по площади (это - отдельная задача, её тут решали много раз). Треугольник АОС состоит из 2 таких треугольников, то есть его площадь равна трети площади АВС.

Но можно и иначе сосчитать - в самом деле, раз АО перпендикулярно DC, то площадь АDC равна АО*DC/2 = 6*12/2 = 36, а площадь ADC равна площади BDC - у них общая высота и равные основания (раз DC - медиана, то AD = DB, само собой). Поэтому площадь АВС равна удвоенной площади ADC, то есть 36*2 = 72.