Задать вопрос Регистрация
Помочь другим

  • y=(x+1)/((x-1)^2) 1)исследовать на четность/нечетность 2)указать промежутки монотонности функции и найти точки экстремумов 3)найти уравнения вертикальных и наклонных ассимптот, используя условия для существования этих ассимптот. построить эти линии на координатной плоскости 4)исследовать поведение функции на концах области определения

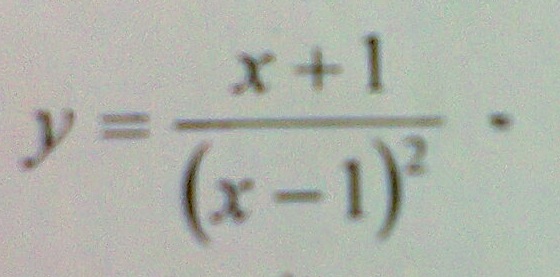
    question img

Ответы 1

  • f(x)=\frac{(x+1)}{(x-1)^2}

    ООФ:

    (x-1)^2eq0\Rightarrow x-1eq0\Rightarrow xeq1\Rightarrow x\in(-\infty;1)\cup(1;+\infty) x=1 - вертикальная ассимптота.

    Чётность/нечётность:

    f(x)=\frac{(x+1)}{(x-1)^2}=\frac{x+1}{x^2-2x+1}\\ f(-x)=\frac{(-x+1)}{(-x-1)^2}=\frac{-x+1}{x^2+2x+1}eq-f(x)eq f(x)

    Функция не является ни чётной, ни нечётной.

    Экстремумы и монотонности:

    f'(x)=\left(\frac{x+1}{(x-1)^2}ight)'=\frac{(x-1)^2-(x+1)(2x-2)}{(x-1)^4}=\frac{-x^2-2x+3}{(x-1)^4}=0\\x_1=1\\-x^2-2x+3=0\\D=4+4\cdot1\cdt3=16\\x_2=\frac{2+4}{-2}=-4\\x_3=\frac{2-4}{-2}=1

    Получаем, что при x<-2 функция убывает, при x=(-2;1),(1;+\infty) - возрастает. То есть, x=-2 - точка минимума.

    Наклонные ассимптоты:

    y=kx+b\\k=$\lim\limits_{x\to \pm\infty}=$\lim\limits_{x\to \pm\infty}\frac{x+1}{(x-1)^2}\cdot1x=0\\b=$\lim\limits_{x\to \pm\infty}f(x)=$\lim\limits_{x\to \pm\infty}\frac{x+1}{(x-1)^2}=$\lim\limits_{x\to \pm\infty}\frac{x(1+\frac1x)}{x^2(1-\frac1x)}=$\lim\limits_{x\to \pm\infty}\frac1x=0

    Следовательно, ни наклонных, ни вертикальных ассимптот функция не имеет.

     

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years