-
нужна срочно помощь.найти область определения!) пример внизу.
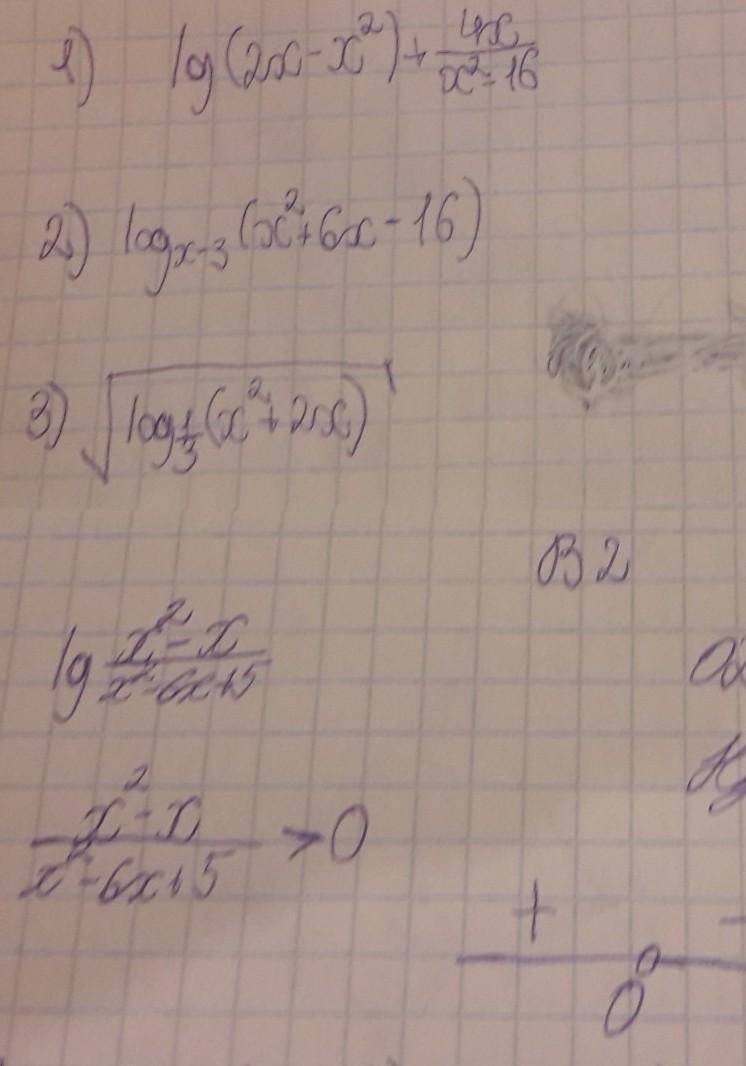
-
Предмет:
Математика -
Автор:
cookie25 - 6 лет назад
-
Ответы 2
-
спасибо;)
-
Автор:
javanojku - 6 лет назад
-
0
-
-
1) 2х-х²>0
х²-16≠0
Эти условия должны выполняться одновременно.
х*(2-х)>0, первое неравенство решим методом интервалов, положительное подлогарифмическое выражение достигается, когда х∈((0;2)), а второе, когда х≠±4, иначе не будет существовать дробь, но в пересечении ОДЗ такая х∈(0;2)
2) х-3≠1
х-3>0
х²+6х-16>0
после преобразования первое условие х≠4
второе х>3
третье тоже решается с помощью метода интервалов,
Найдем корни левой части неравенства
х₁,₂=-3±√(9+16)=-3±5 Корни -8 и 2 разобьют область определения на интервалы (-∞;-8);(-8;2);(2;+∞) установим знаки на каждом из них.
Положительный трехчлен при х∈(-∞;-8)∪(2;+∞)
Найдем теперь пересечение всех трех условий. т.е. одновременное их выполнение. ОДЗ получим (3;4)∪(4;+∞)
3) подкоренное выражение неотрицательно, когда ㏒₁/₃(х²+2х)≥0, второе условие (х²+2х)>0
Чтобы решить неравенство первое, вспомним, что логарифм. функция при основании одна треть будет убывающей, поэтому
х²+2х≤(1/3)°, х²+2х-1≤0
Приравняем к нулю левую часть. х²+2х-1=0
х₁,₂=-1±√(1+1)
Корни -1-√2 и -1+√2 разобьют обл. опр. на интервалы
(-∞;-1-√2);(-1-√2;-1+√2);(-1+√2;+∞)
Решением неравенства х²+2х-1≤0 будет отрезок [-1-√2;-1+√2], а решением неравенства (х²+2х)>0, или х*(х+2)>0 будет объединение интервалов (-∞;-2)∪(2;+∞)
А ОДЗ - это пересечение двух решений. Им будет
[-1-√2;-2)∪(0;-1+√2]
-
Автор:
chanceandrews - 6 лет назад
-
0
-
-
Добавить свой ответ
-
write a few sentences about gestures a tourist should avoid using while in your contry. (Belarus or Russia)
-
Предмет:
Английский язык -
Автор:
angel15 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
- Реактивний литак ту 154,политае над лісом за 1 хв, визначити довжину лісу в напрямку полйоту літака його швидкість 850 км на год,, помогите решить пожалуйста
-
ПОЖАЛУЙСТА ПОМОГИТЕ!!!
Стальной баллон объемом 100 л заполнен влажным кислородом под давлением 10,13 * 105 Па. Через год давление внутри баллона упало до 9 * 105 Па.
Рассчитать количество прокорродировавшего металла и написать управление коррозионного процесса. Парциальным давлением паров воды пренебречь.
-
Предмет:
Другие предметы -
Автор:
cannonifbl - 6 лет назад
-
Ответов:
6 -
Смотреть
-
-
Сумма первых n членов арифметической прогрессии вычисляется по формуле Sn=(a1+an)2·n. Пользуясь этой формулой, вычисли значение a1, если an=2, Sn=228, n=12.
Ответ: .-
Предмет:
Математика -
Автор:
rambomoses - 6 лет назад
-
Ответов:
0 -
Смотреть
-
