-
С линиями, заданными следующими уравнениями вычислить грань ограниченной формы.
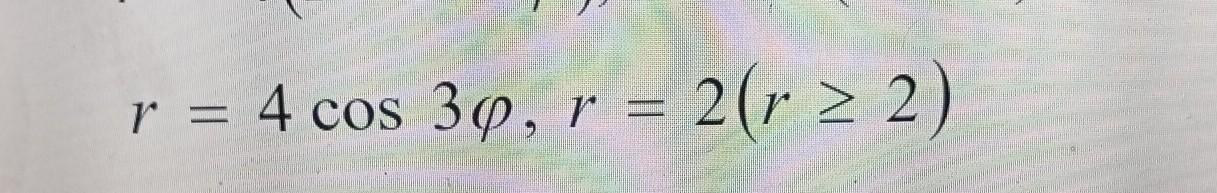
-
Предмет:
Математика -
Автор:
kody - 2 года назад
-
Ответы 1
-
Ответ:
Для вычисления грани ограниченной формы, заданной уравнениями, необходимо найти область пересечения этих уравнений.
Уравнение $r = 4 \cos 3\varphi$ задает полярную кривую, которая представляет собой лепесток розы с тремя лепестками. Здесь $r$ - расстояние от начала координат до точки на кривой, а $\varphi$ - угол между положительным направлением оси $x$ и линией, соединяющей начало координат и точку на кривой.
Уравнение $r = 2$ задает окружность радиусом 2 с центром в начале координат.
Чтобы найти грань ограниченной формы, нужно найти точки пересечения этих двух кривых. Подставим уравнение окружности в уравнение лепестка розы:
$2 = 4 \cos 3\varphi$
Разделим обе части уравнения на 4:
$\frac{1}{2} = \cos 3\varphi$
Теперь найдем значения угла $\varphi$, для которых выполняется это уравнение. Используя обратную функцию косинуса, получим:
$3\varphi = \arccos \left(\frac{1}{2}\right)$
$\varphi = \frac{1}{3} \arccos \left(\frac{1}{2}\right)$
Таким образом, грань ограниченной формы будет представлять собой сегмент лепестка розы, ограниченный углами $\varphi = 0$ и $\varphi = \frac{1}{3} \arccos \left(\frac{1}{2}\right)$.
-
Автор:
cheyennelarson - 2 года назад
-
10
-
-
Добавить свой ответ
-
Освободить от иррациональности в знаменатели дроби, хочу себя проверить 15/3√5. 4/5√4. 14/3√49 пожалуйста
-
Предмет:
Математика -
Автор:
vikakitaki0 - 2 года назад
-
Ответов:
1 -
Смотреть
-
- Речовина віддає теплоту, але температура її не змінюється. Який процес відбувається? дифузії плавлення кристалізації нагрівання охолодження
-
Мама решила набрать вес в 30 лет, чтобы у неё выросла грудь. Как думаете, чем это закончилось? Ей сейчас 37, рост 169 см
-
Предмет:
Другие предметы -
Автор:
charlie100 - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
9. Знайди чотири послідовних цілих числа, якщо добуток двох більших з них на
78 більший за добуток двох менших
-
Предмет:
Алгебра -
Автор:
audreymitchell - 2 года назад
-
Ответов:
1 -
Смотреть
-
